二項分布と超幾何分布
二項分布
- 抽出方法: 復元抽出
- 試行の独立性: 各試行は独立
- 確率: 各試行で成功確率は一定
超幾何分布
- 抽出方法: 非復元抽出
- 試行の独立性: 各試行は独立していない
- 確率: 各試行で成功確率が変化
グラフの比較
今回の実験では、二項分布と超幾何分布の違いを視覚的に比較します。二項分布は、復元抽出を行う場合に適用され、各試行が独立しており、成功確率が一定です。一方、超幾何分布は、非復元抽出を行う場合に適用され、試行ごとに成功確率が変化します。実験では、母集団のサイズ、成功対象の数、抽出回数を変え、それぞれのグラフを描画します。特に、サンプルサイズが大きい場合や母集団が小さい場合など、分布の形状に顕著な違いが現れる条件に注目して比較を行います。これにより、抽出方法による分布の違いを視覚的に確認し、二項分布と超幾何分布の特性を理解します。
復元抽出と非復元抽出の比較(広範囲のパラメータ設定)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# パラメータ比を一定に保ったグラフを作成
M_values = [50, 150, 250, 350, 450]
N_A_values = [15, 45, 75, 105, 135] # M の 30%
n_values = [7, 22, 37, 52, 67] # M の 15%
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(5, 1, figsize=(10, 30))
# 異なるパラメータ設定でグラフを描画
for i in range(5):
plot_comparison(M=M_values[i], N_A=N_A_values[i], n=n_values[i], ax=axs[i])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()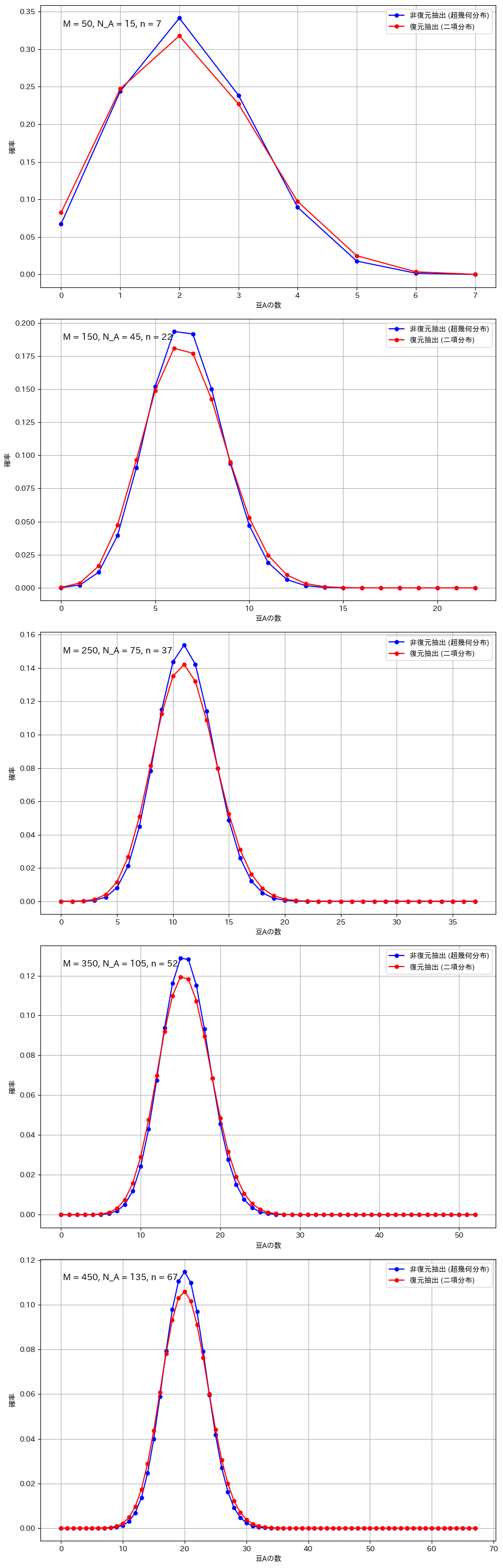
復元抽出と非復元抽出の比較(顕著な違いが現れる条件)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(3, 1, figsize=(10, 18)) # 高さを調整
# 条件1: サンプルサイズが大きい場合
plot_comparison(M=100, N_A=30, n=80, ax=axs[0])
# 条件2: 全体のサイズが小さい場合
plot_comparison(M=20, N_A=6, n=15, ax=axs[1])
# 条件3: 極端な割合の場合
plot_comparison(M=100, N_A=90, n=30, ax=axs[2])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()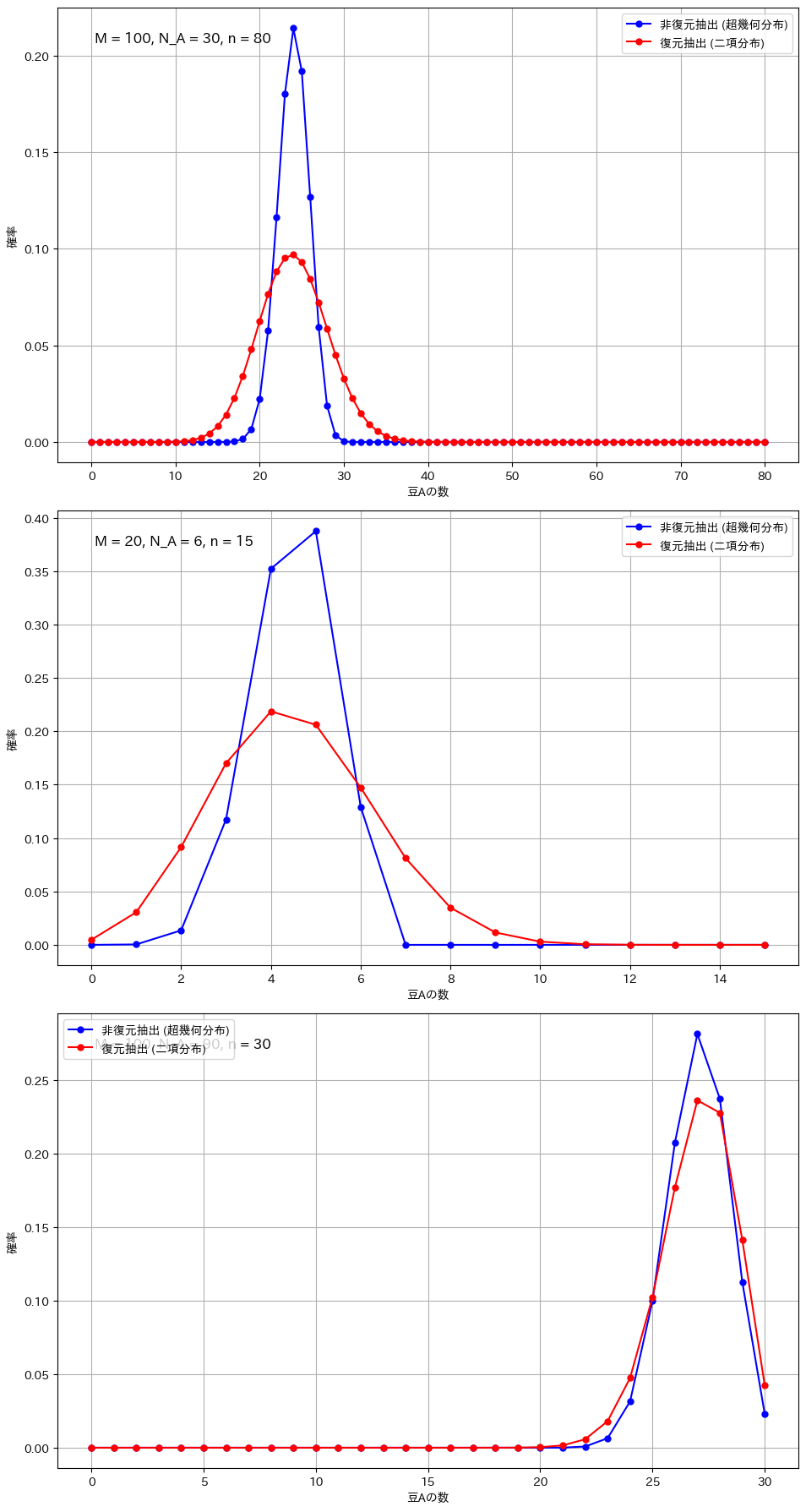
考察
二項分布と超幾何分布の違いが顕著になるのは、サンプルサイズが全体に対して大きい場合や、母集団が小さい場合です。例えば、全体の豆の数が100個で80個を抽出する場合や、母集団が20個でそのうち15個を抽出する場合、非復元抽出では次の試行に与える影響が大きくなり、復元抽出との差が明確に現れます。また、成功確率が極端に高いか低い場合も、非復元抽出の影響で分布が変わりやすくなります。一方、サンプルサイズが小さい場合や母集団が非常に大きい場合には、各抽出の影響が少なく、二項分布と超幾何分布の違いは目立たなくなります。
混合ガウスモデルによる観測データの分布特性推定
概要:
本実験では、観測データが複数の異なる分布の混合によって生成されている可能性を考慮し、その分布特性を推定する手法を検証する。具体的には、2つの正規分布を混合したデータを生成し、EMアルゴリズムを用いてその混合ガウスモデルをフィッティングする。実験の結果、生成されたデータの背後にある各分布の平均、標準偏差、および混合割合を高精度に推定できることを確認した。本手法は、複雑な観測データに対する分布特性の解析やデータの要因分解に有効である。
2つの成分
import numpy as np
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 1. データ生成: 混合正規分布から乱数を生成
np.random.seed(0)
n_samples = 1000
# 2つの正規分布のパラメータ設定
mean1, std1 = 0, 1 # 正規分布1
mean2, std2 = 5, 1.5 # 正規分布2
weight1, weight2 = 0.4, 0.6 # 混合割合
# 2つの分布からデータ生成
data1 = np.random.normal(mean1, std1, int(weight1 * n_samples))
data2 = np.random.normal(mean2, std2, int(weight2 * n_samples))
# 混合データの作成
data = np.hstack([data1, data2])
np.random.shuffle(data)
# 2. 混合モデルの構築とフィッティング (EMアルゴリズムを使用)
gmm = GaussianMixture(n_components=2, random_state=0)
gmm.fit(data.reshape(-1, 1))
# 推定されたパラメータ
means = gmm.means_.flatten()
std_devs = np.sqrt(gmm.covariances_).flatten()
weights = gmm.weights_
print("推定された平均:", means)
print("推定された標準偏差:", std_devs)
print("推定された混合割合:", weights)
# 3. 結果のプロット
x = np.linspace(-3, 10, 1000)
pdf1 = weights[0] * (1 / (std_devs[0] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[0])**2 / (2 * std_devs[0]**2)))
pdf2 = weights[1] * (1 / (std_devs[1] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[1])**2 / (2 * std_devs[1]**2)))
plt.hist(data, bins=30, density=True, alpha=0.5, color='gray', label='データのヒストグラム')
plt.plot(x, pdf1 + pdf2, 'r-', lw=2, label='フィッティングされたモデル')
plt.plot(x, pdf1, 'b--', lw=2, label='成分 1')
plt.plot(x, pdf2, 'g--', lw=2, label='成分 2')
plt.title('データとフィッティングされた混合ガウスモデル')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()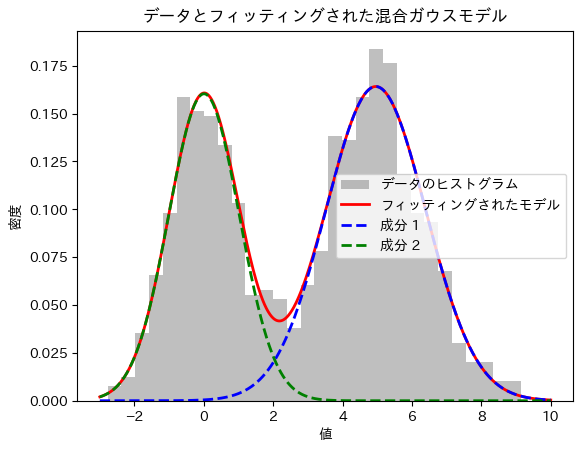
3つの成分
import numpy as np
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 1. データ生成: 混合正規分布から乱数を生成
np.random.seed(0)
n_samples = 1000
# 3つの正規分布のパラメータ設定
mean1, std1 = 0, 1 # 正規分布1
mean2, std2 = 5, 1.5 # 正規分布2
mean3, std3 = 10, 2 # 正規分布3
weight1, weight2, weight3 = 0.3, 0.4, 0.3 # 混合割合
# 3つの分布からデータ生成
data1 = np.random.normal(mean1, std1, int(weight1 * n_samples))
data2 = np.random.normal(mean2, std2, int(weight2 * n_samples))
data3 = np.random.normal(mean3, std3, int(weight3 * n_samples))
# 混合データの作成
data = np.hstack([data1, data2, data3])
np.random.shuffle(data)
# 2. 混合モデルの構築とフィッティング (EMアルゴリズムを使用)
gmm = GaussianMixture(n_components=3, random_state=0)
gmm.fit(data.reshape(-1, 1))
# 推定されたパラメータ
means = gmm.means_.flatten()
std_devs = np.sqrt(gmm.covariances_).flatten()
weights = gmm.weights_
print("推定された平均:", means)
print("推定された標準偏差:", std_devs)
print("推定された混合割合:", weights)
# 3. 結果のプロット
x = np.linspace(-5, 15, 1000)
pdf1 = weights[0] * (1 / (std_devs[0] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[0])**2 / (2 * std_devs[0]**2)))
pdf2 = weights[1] * (1 / (std_devs[1] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[1])**2 / (2 * std_devs[1]**2)))
pdf3 = weights[2] * (1 / (std_devs[2] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[2])**2 / (2 * std_devs[2]**2)))
plt.hist(data, bins=30, density=True, alpha=0.5, color='gray', label='データのヒストグラム')
plt.plot(x, pdf1 + pdf2 + pdf3, 'r-', lw=2, label='フィッティングされたモデル')
plt.plot(x, pdf1, 'b--', lw=2, label='成分 1')
plt.plot(x, pdf2, 'g--', lw=2, label='成分 2')
plt.plot(x, pdf3, 'y--', lw=2, label='成分 3')
plt.title('データとフィッティングされた混合ガウスモデル')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()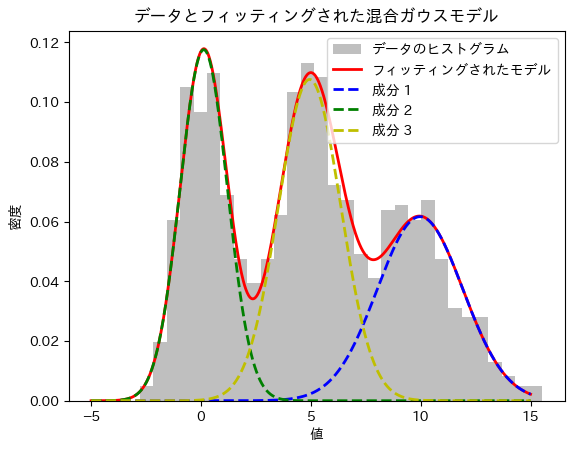
独立な指数分布に従う2変数の和の確率
指数分布の和はガンマ分布に従います。
X1,X2は互いに独立でパラメータλを持つ指数分布に従います。
U=X1+X2とします
数式を使ってUの確率密度関数を求めます。
import sympy as sp
# 変数の定義
x, u, lambda_value = sp.symbols('x u lambda', positive=True, real=True)
# 指数分布の確率密度関数 (PDF) f(x)
f_x = lambda_value * sp.exp(-lambda_value * x)
# 畳み込み積分を計算して、g(u) = f(x) * f(u - x) の形式にする
g_u = sp.integrate(f_x * lambda_value * sp.exp(-lambda_value * (u - x)), (x, 0, u))
# 簡略化
g_u_simplified = sp.simplify(g_u)
# 結果の表示
display(g_u_simplified)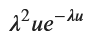
求まりました。
X1 (X2)と、Uの確率密度関数を重ねて描画してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2 の範囲
# X1, X2 の指数分布の確率密度関数 (PDF) - 同じなので1つにまとめる
pdf_X1_X2 = lambda_value * np.exp(-lambda_value * x_range)
# U = X1 + X2 は形状パラメータk=2、スケールパラメータθ=1/λのガンマ分布
u_range = np.linspace(0, 10, 1000)
pdf_U = gamma.pdf(u_range, a=2, scale=1/lambda_value)
# グラフのプロット
plt.figure(figsize=(8, 6))
# X1 (X2) の指数分布の描画
plt.plot(x_range, pdf_X1_X2, label='X1 (X2) (指数分布)', color='blue', linestyle='--')
# U のガンマ分布の描画
plt.plot(u_range, pdf_U, label='U = X1 + X2 (ガンマ分布)', color='red')
# グラフの装飾
plt.title('X1 (X2) と U の確率密度関数の比較')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.show()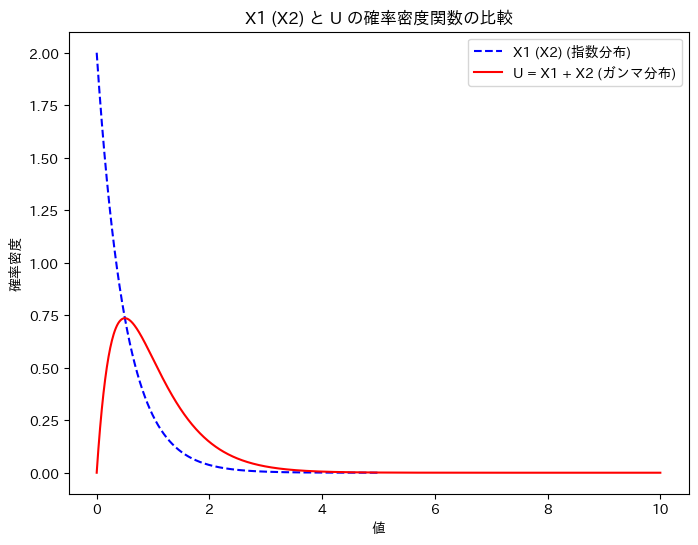
グラフの形状から、U = X1 + X2の関係は想像しづらいですね。
ガンマ分布の形状パラメータを1~2に変化させて、X1 (X2)からUへの変化を確認します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2, U の範囲を0~5に設定
# ガンマ分布の形状パラメータを1から2まで0.1ずつ変化させる
shape_params = np.arange(1, 2.1, 0.1) # 1から2までの形状パラメータを0.1ステップで変化
# グラフのプロット
plt.figure(figsize=(8, 6))
# 形状パラメータが1から2に変化するガンマ分布の描画
for k in shape_params:
gamma_pdf = gamma.pdf(x_range, a=k, scale=1/lambda_value)
plt.plot(x_range, gamma_pdf, label=f'形状パラメータ k={k:.1f}')
# X1 (X2) の指数分布の描画 - 同じなので1つにまとめる
pdf_X1_X2 = lambda_value * np.exp(-lambda_value * x_range)
plt.plot(x_range, pdf_X1_X2, label='X1 (X2) (指数分布)', color='blue', linestyle='--')
# グラフの装飾
plt.title('指数分布からガンマ分布への変化 (形状パラメータの0.1ステップ変化)')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.show()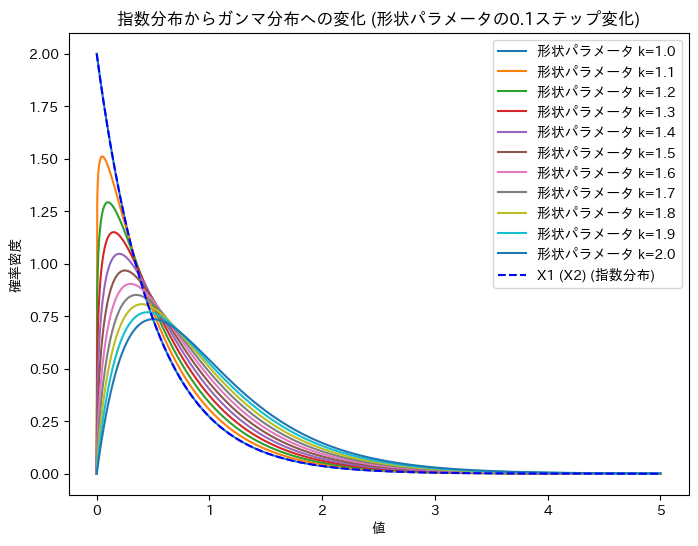
X1 (X2)からUへの変化が可視化できました。
次に、X1 (X2)と、Uの累積分布関数を重ねて描画してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon, gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2 の範囲
# X1, X2 の指数分布の累積分布関数 (CDF) - 同じなので1つにまとめる
cdf_X1_X2 = expon.cdf(x_range, scale=1/lambda_value)
# U = X1 + X2 は形状パラメータk=2、スケールパラメータθ=1/λのガンマ分布
u_range = np.linspace(0, 10, 1000)
cdf_U = gamma.cdf(u_range, a=2, scale=1/lambda_value)
# グラフのプロット
plt.figure(figsize=(8, 6))
# X1 (X2) の指数分布のCDFの描画
plt.plot(x_range, cdf_X1_X2, label='X1 (X2) (指数分布 CDF)', color='blue', linestyle='--')
# U のガンマ分布のCDFの描画
plt.plot(u_range, cdf_U, label='U = X1 + X2 (ガンマ分布 CDF)', color='red')
# グラフの装飾
plt.title('X1 (X2) と U の累積分布関数 (CDF) の比較')
plt.xlabel('値')
plt.ylabel('累積確率')
plt.legend()
# グラフの表示
plt.show()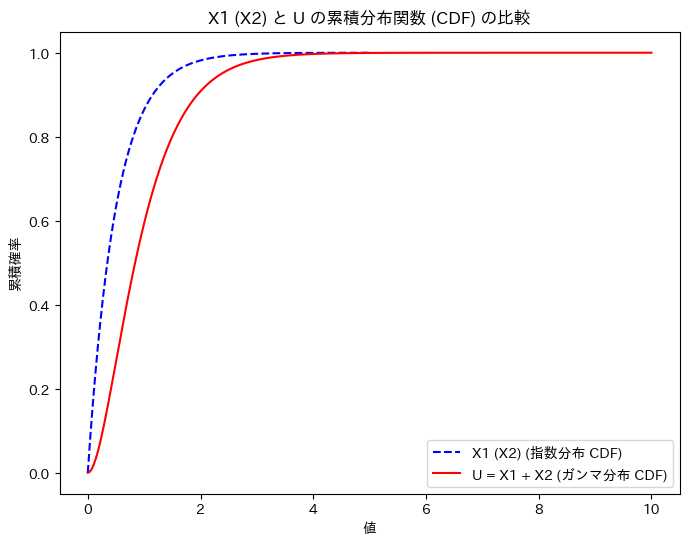
グラフの形状から、U = X1 + X2の関係を想像しやすくなりました。
豆の非復元抽出
豆の非復元抽出は超幾何分布になる
豆の実験の概要
この実験は、100個の豆が入った袋の中から無作為に15個の豆を取り出し、その中に含まれる特定の種類の豆(豆A)の数を調べるシミュレーションを通じて、超幾何分布がどのように現実の状況を表現するかを確認するものです。
実験の設定:
- 袋の中の豆の総数: 100個
- 豆Aの数: 30個
- 豆Bの数: 70個
- 取り出す豆の数: 15個
実験の手順:
- 袋に入っている100個の豆のうち、30個が豆Aであり、残り70個が豆Bであるとします。
- 袋から無作為に15個の豆を非復元で抽出し、その中に含まれる豆Aの数を数えます。
- この抽出操作を10000回繰り返し、各回で得られた豆Aの数を記録します。
- 記録されたデータを基に、豆Aの数の分布をヒストグラムとして描画し、理論的に計算された超幾何分布と比較します。
実験の目的:
- この実験の目的は、理論的な超幾何分布が、豆を無作為に非復元抽出した際の豆Aの数の分布をどの程度正確に表現できるかを確認することです。
- 結果として得られるシミュレーションの分布が、理論的な超幾何分布とよく一致することが期待されます。これにより、超幾何分布が現実の非復元抽出を扱う際に有効であることが示されます。
結果の分析:
- シミュレーションの結果と理論的な超幾何分布を比較することで、両者の一致度を確認します。
- この実験は、非復元抽出のシナリオで生じる確率分布が、理論的な超幾何分布に従うことを実証的に示すものです。
シミュレーションによる計算
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import hypergeom
# パラメータの設定
M = 100 # 全体の豆の数
N_A = 30 # 豆Aの数
n = 15 # 抽出する豆の数
x_values = np.arange(0, n+1) # 可能な豆Aの数
# 理論的な超幾何分布のPMFを計算
rv = hypergeom(M, N_A, n)
pmf_theoretical = rv.pmf(x_values)
# 数値シミュレーションの設定
n_simulations = 10000 # シミュレーション回数
simulated_counts = []
# シミュレーションの実行
for _ in range(n_simulations):
# 袋の中の豆を表すリスト(1が豆A、0が豆B)
bag = np.array([1]*N_A + [0]*(M - N_A))
# 無作為に15個抽出
sample = np.random.choice(bag, size=n, replace=False)
# 抽出した中の豆Aの数をカウント
count_A = np.sum(sample)
simulated_counts.append(count_A)
# シミュレーションから得られたPMFを計算
pmf_simulated, bins = np.histogram(simulated_counts, bins=np.arange(-0.5, n+1.5, 1), density=True)
# グラフの描画
plt.figure(figsize=(10, 6))
# 理論的なPMFの描画
plt.plot(x_values, pmf_theoretical, 'bo-', label='理論的PMF', markersize=8)
# シミュレーション結果をヒストグラムとして描画
plt.hist(simulated_counts, bins=np.arange(-0.5, n+1.5, 1), density=True, alpha=0.5, color='red', label='シミュレーション結果')
# グラフの設定
plt.xlabel('豆Aの数')
plt.ylabel('確率')
plt.title('超幾何分布のPMF: 理論とシミュレーションの比較')
plt.legend()
plt.grid(True)
plt.show()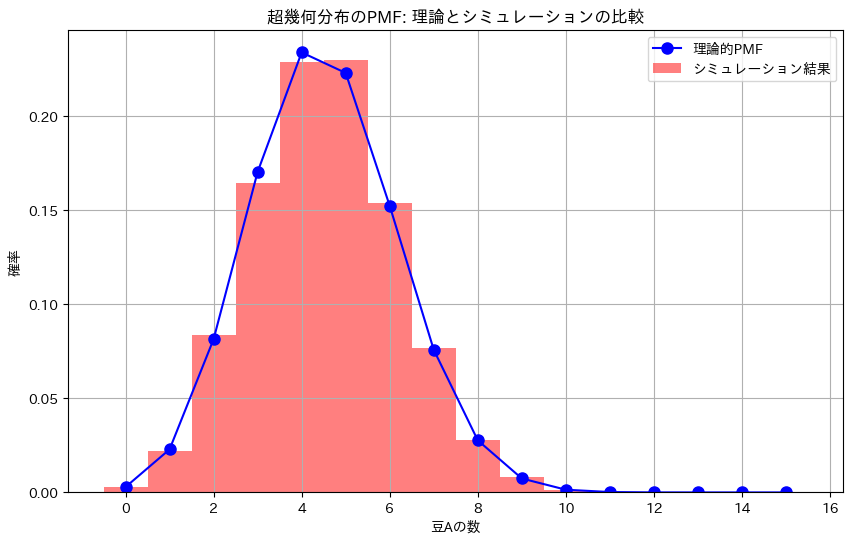
負の二項分布
ポアソン-ガンマ混合分布は、負の二項分布になる
数式を使った計算
import sympy as sp
# 定義
k = sp.symbols('k', integer=True)
alpha, beta = sp.symbols('alpha beta', positive=True)
lambda_var = sp.symbols('lambda', positive=True)
# ポアソン分布の確率質量関数
poisson_pmf = (lambda_var**k * sp.exp(-lambda_var)) / sp.factorial(k)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha - 1) * sp.exp(-beta * lambda_var)
# 周辺分布の計算
marginal_distribution = sp.integrate(poisson_pmf * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
marginal_distribution
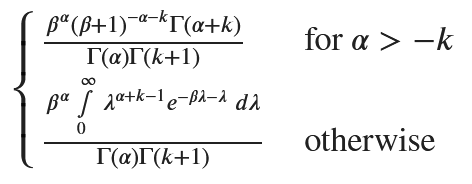
次式と同じなので、負の二項分布となる。

シミュレーションによる計算
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma, nbinom
# パラメータの設定
alpha = 3.0
beta = 2.0
sample_size = 10000
# ガンマ分布から λ を生成
lambda_samples = np.random.gamma(alpha, 1/beta, sample_size)
# 生成された λ を使ってポアソン分布から X を生成
poisson_samples = [np.random.poisson(lam) for lam in lambda_samples]
# 負の二項分布のパラメータを設定
r = alpha
p = beta / (beta + 1)
# 負の二項分布から理論的な確率質量関数を計算
x = np.arange(0, max(poisson_samples) + 1)
nbinom_pmf = nbinom.pmf(x, r, p)
# ヒストグラムの描画
plt.hist(poisson_samples, bins=np.arange(0, max(poisson_samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black', rwidth=0.8)
# 理論的な負の二項分布の確率質量関数をプロット
plt.plot(x, nbinom_pmf, 'r', linestyle='-', label='理論的な負の二項分布')
# グラフのタイトルとラベル
plt.title('ポアソン-ガンマ混合分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()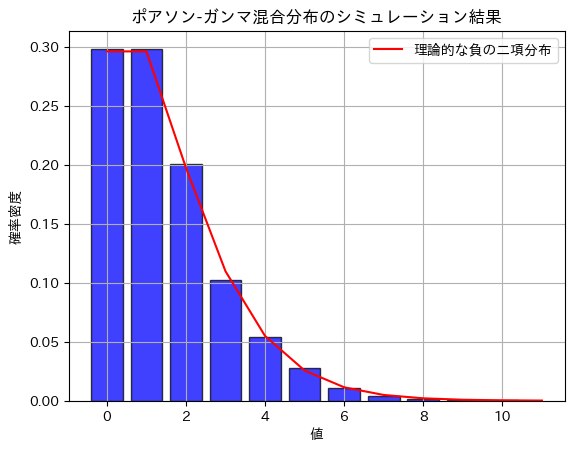
ガンマ分布
ガンマ分布の期待値と分散の導出
数式を使った計算
import sympy as sp
# 定義
lambda_var = sp.symbols('lambda')
alpha, beta = sp.symbols('alpha beta', positive=True)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha-1) * sp.exp(-beta * lambda_var)
# 期待値 E[Λ] の計算
expected_value = sp.integrate(lambda_var * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# E[Λ^2] の計算
expected_value_Lambda2 = sp.integrate(lambda_var**2 * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# 分散 V[Λ] の計算
variance = (expected_value_Lambda2 - expected_value**2).simplify()
# 結果を辞書形式で表示
{
"期待値 E[Λ]": expected_value,
"分散 V[Λ]": variance
}{'期待値 E[Λ]': alpha/beta, '分散 V[Λ]': alpha/beta**2}シミュレーションによる計算
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# サンプルサイズ
sample_size = 10000
# ガンマ分布に従う乱数を生成
samples = np.random.gamma(alpha, 1/beta, sample_size)
# 期待値と分散の計算
expected_value = np.mean(samples)
variance = np.var(samples)
# 結果の表示
print(f"期待値のシミュレーション結果: {expected_value}")
print(f"分散のシミュレーション結果: {variance}")
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なガンマ分布の確率密度関数をプロット
x = np.linspace(0, max(samples), 100)
gamma_pdf = gamma.pdf(x, alpha, scale=1/beta)
plt.plot(x, gamma_pdf, 'r', linestyle='-', label='理論的なガンマ分布')
# グラフのタイトルとラベル
plt.title('ガンマ分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()期待値のシミュレーション結果: 1.4947527551017439
分散のシミュレーション結果: 0.7452822182213243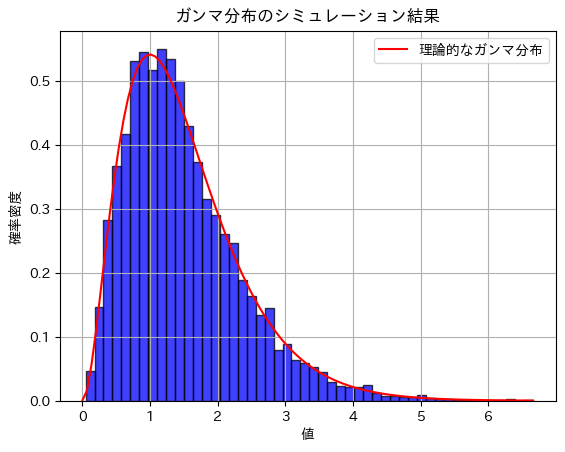
シミュレーションによる計算 (ガンマ分布に従う乱数生成関数をスクラッチで記述)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
def custom_exponential(beta):
# [0, 1) の一様乱数を生成
u = np.random.rand()
# 指数分布に従う乱数を生成
return -np.log(u) / beta
def custom_gamma(alpha, beta, sample_size):
samples = []
for _ in range(sample_size):
sample = sum(custom_exponential(beta) for _ in range(int(alpha)))
samples.append(sample)
return samples
# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# サンプルサイズ
sample_size = 10000
# カスタム関数を使ってガンマ分布に従う乱数を生成
samples = custom_gamma(alpha, beta, sample_size)
# 期待値と分散の計算
expected_value = np.mean(samples)
variance = np.var(samples)
# 理論値
theoretical_expected_value = alpha / beta
theoretical_variance = alpha / beta**2
# 結果の表示
print(f"シミュレーション結果 - 期待値: {expected_value}, 理論値: {theoretical_expected_value}")
print(f"シミュレーション結果 - 分散: {variance}, 理論値: {theoretical_variance}")
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なガンマ分布の確率密度関数をプロット
x = np.linspace(0, max(samples), 100)
gamma_pdf = gamma.pdf(x, alpha, scale=1/beta)
plt.plot(x, gamma_pdf, 'r', linestyle='-', label='理論的なガンマ分布')
# グラフのタイトルとラベル
plt.title('ガンマ分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()
シミュレーション結果 - 期待値: 1.4966126702823181, 理論値: 1.5
シミュレーション結果 - 分散: 0.7242038142114708, 理論値: 0.75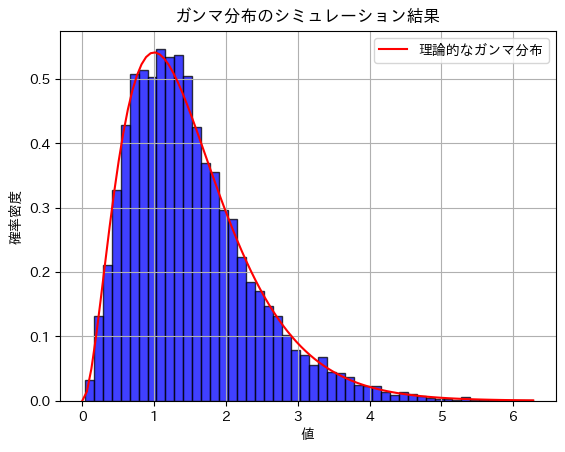
ポアソン分布
ポアソン分布の期待値と分散の導出
数式を使った計算
import sympy as sp
# 定義
k = sp.symbols('k')
lambda_param = sp.symbols('lambda')
# ポアソン分布の確率関数
poisson_pmf = (lambda_param**k * sp.exp(-lambda_param)) / sp.factorial(k)
# 期待値 E[X] の計算
expected_value = sp.summation(k * poisson_pmf, (k, 0, sp.oo)).simplify()
# E[X^2] の計算
expected_value_X2 = sp.summation(k**2 * poisson_pmf, (k, 0, sp.oo)).simplify()
# 分散 V[X] の計算
variance = (expected_value_X2 - expected_value**2).simplify()
# 結果を表示
{
"期待値 E[X]": expected_value,
"分散 V[X]": variance
}{'期待値 E[X]': lambda, '分散 V[X]': lambda}シミュレーションによる計算
import numpy as np
# パラメータ λ の設定
lambda_param = 5
# シミュレーションの回数
num_simulations = 10000
# 各シミュレーションで生成するサンプルの数
sample_size = 1000
# シミュレーション結果の保存用
expected_values = []
variances = []
for _ in range(num_simulations):
# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)
# 期待値を計算
expected_values.append(np.mean(samples))
# 分散を計算
variances.append(np.var(samples))
# シミュレーション結果の平均を計算
average_expected_value = np.mean(expected_values)
average_variance = np.mean(variances)
print(f"期待値のシミュレーション結果: {average_expected_value}")
print(f"分散のシミュレーション結果: {average_variance}")期待値のシミュレーション結果: 4.999602
分散のシミュレーション結果: 4.9992533574プロット
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
# パラメータ λ の設定
lambda_param = 5
# サンプルサイズ
sample_size = 10000
# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)
# ヒストグラムの描画
plt.hist(samples, bins=np.arange(0, max(samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なポアソン分布の確率質量関数をプロット
x = np.arange(0, max(samples) + 1)
poisson_pmf = (lambda_param**x * np.exp(-lambda_param)) / factorial(x)
plt.plot(x, poisson_pmf, 'r', marker='o', linestyle='-', label='理論的なポアソン分布')
# グラフのタイトルとラベル
plt.title('ポアソン分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()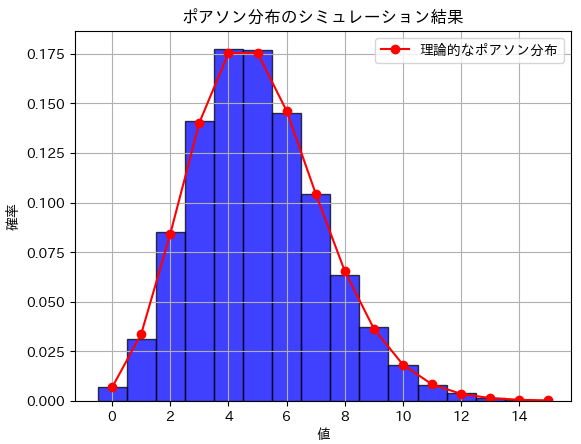
シミュレーションによる計算 (ポアソン分布に従う乱数生成関数をスクラッチで記述)
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
def custom_poisson(lambda_param, sample_size):
samples = []
for _ in range(sample_size):
k = 0
p = np.exp(-lambda_param)
sum_p = p
u = np.random.rand()
while u > sum_p:
k += 1
p *= lambda_param / k
sum_p += p
samples.append(k)
return samples
# パラメータ λ の設定
lambda_param = 5
# サンプルサイズ
sample_size = 10000
# カスタム関数を使ってポアソン分布に従う乱数を生成
samples = custom_poisson(lambda_param, sample_size)
# ヒストグラムの描画
plt.hist(samples, bins=np.arange(0, max(samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なポアソン分布の確率質量関数をプロット
x = np.arange(0, max(samples) + 1)
poisson_pmf = (lambda_param**x * np.exp(-lambda_param)) / factorial(x)
plt.plot(x, poisson_pmf, 'r', marker='o', linestyle='-', label='理論的なポアソン分布')
# グラフのタイトルとラベル
plt.title('ポアソン分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()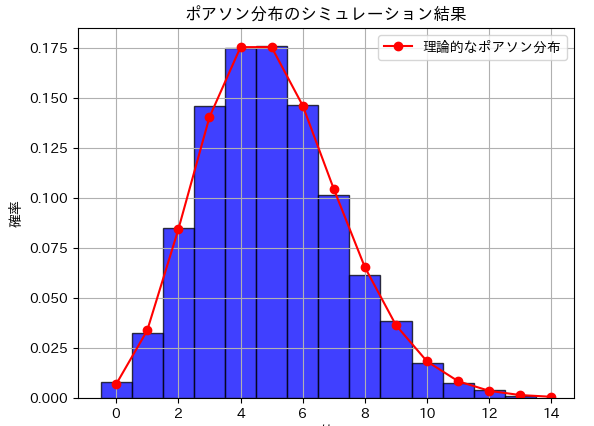
乱数生成のプロセス
- 初期化:
kを 0 に設定します(ポアソン分布の乱数)。pを exp(−λ)に設定します(初期確率)。sum_pをpに設定します。uを [0, 1) の一様乱数として生成します。
- 累積確率と乱数の比較:
uがsum_pより大きい間、以下のステップを繰り返します。kを増加させます。pを更新し、累積確率sum_pに追加します。
- サンプル追加:
- ループが終了すると、
kをsamplesリストに追加します。
- ループが終了すると、
この方法により、ポアソン分布に従う乱数を自作関数で生成することができます。他に質問があれば、お知らせください。
確率空間の事象 A,B,CのP(A∩B∩C)のとり得る範囲
問
確率空間の事象 A,B,C の確率がそれぞれ P(A) = P(B) = P(C) = ![]()
かつ P(A∩B)=P(A)P(B) , P(A∩C)=P(A)P(C) , P(B∩C)=P(B)P(C)
のとき、P(A∩B∩C)のとり得る範囲は?
解き方
A、B、Cのベン図が持つ8個のエリアに対して16個の点を配置し、特定の確率条件を満たす事象の組み合わせをシミュレーションによって求める。事象A、B、Cの個別確率およびそれらの共通部分の確率を基に、各エリアに属する点数の全ての可能な組み合わせを探索する。各組み合わせについて計算を行い、条件を満たす場合はその組み合わせをリストに追加し、最小値と最大値を更新する。最終的に、条件を満たす最小および最大の値を特定し、それぞれの点数の組み合わせを明らかにする。結果として、条件を満たす最小値と最大値に対応する具体的な点数の配分が得られる。
コード
# 定数
total_points = 16
PA = 3 / 4
PB = 3 / 4
PC = 3 / 4
PAB = 9 / 16
PAC = 9 / 16
PBC = 9 / 16
# 結果を格納するリスト
valid_probabilities = []
# 最小値と最大値を取るときの組み合わせを格納する変数
min_combination = None
max_combination = None
min_value = float('inf')
max_value = float('-inf')
# 各エリアの点数の範囲を狭める
for n1 in range(total_points // 3 + 1):
for n2 in range((total_points - 3 * n1) // 3 + 1):
for n3 in range(total_points - 3 * n1 - 3 * n2 + 1):
n4 = total_points - 3 * n1 - 3 * n2 - n3
if n4 < 0:
continue
calc_PA = (n1 + 2 * n2 + n4) / total_points
calc_PB = (n1 + 2 * n2 + n4) / total_points
calc_PC = (n1 + 2 * n2 + n4) / total_points
calc_PAB = (n2 + n4) / total_points
calc_PAC = (n2 + n4) / total_points
calc_PBC = (n2 + n4) / total_points
# 条件を満たすか確認
if (abs(calc_PA - PA) < 1e-9 and
abs(calc_PB - PB) < 1e-9 and
abs(calc_PC - PC) < 1e-9 and
abs(calc_PAB - PAB) < 1e-9 and
abs(calc_PAC - PAC) < 1e-9 and
abs(calc_PBC - PBC) < 1e-9):
current_PABC = n4 / total_points
valid_probabilities.append(current_PABC)
if current_PABC < min_value:
min_value = current_PABC
min_combination = (n1, n2, n3, n4)
if current_PABC > max_value:
max_value = current_PABC
max_combination = (n1, n2, n3, n4)
# 最小値と最大値を表示
min_PABC = min_value if valid_probabilities else None
max_PABC = max_value if valid_probabilities else None
# 結果の表示
print(f"最小値: {min_PABC}")
print(f"最大値: {max_PABC}")
print(f"最小値を取るときのN1, N2, N3, N4: {min_combination}")
print(f"最大値を取るときのN1, N2, N3, N4: {max_combination}")
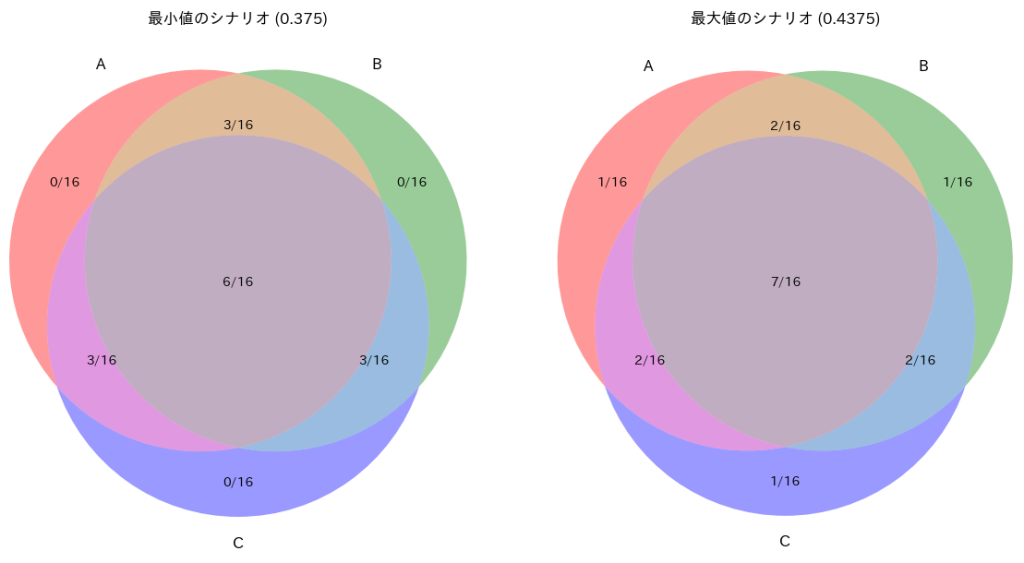
最小値: 0.375
最大値: 0.4375
最小値を取るときのN1, N2, N3, N4: (0, 3, 1, 6)
最大値を取るときのN1, N2, N3, N4: (1, 2, 0, 7)