二項分布の確率母関数
、その1階微分 
、および2階微分 
を視覚的に比較してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative
# パラメータ設定
n = 10 # 試行回数
p = 0.5 # 成功確率
# 確率母関数 G_X(t)
def G_X(t, n, p):
return (p * t + (1 - p))**n
# 1階微分 G'_X(t)
def G_X_diff_1(t, n, p):
return derivative(lambda t: G_X(t, n, p), t, dx=1e-6)
# 2階微分 G''_X(t)
def G_X_diff_2(t, n, p):
return derivative(lambda t: G_X_diff_1(t, n, p), t, dx=1e-6)
# t の範囲を定義
t_values = np.linspace(0, 1, 100)
# G_X(t), G'_X(t), G''_X(t) の値を計算
G_X_values = [G_X(t, n, p) for t in t_values]
G_X_diff_1_values = [G_X_diff_1(t, n, p) for t in t_values]
G_X_diff_2_values = [G_X_diff_2(t, n, p) for t in t_values]
# グラフの描画
plt.plot(t_values, G_X_values, label="G_X(t) (確率母関数)", color="blue")
plt.plot(t_values, G_X_diff_1_values, label="G'_X(t) (1階微分)", color="green")
plt.plot(t_values, G_X_diff_2_values, label="G''_X(t) (2階微分)", color="red")
plt.title(f"G_X(t), G'_X(t), G''_X(t) の比較 (n={n}, p={p})")
plt.xlabel("t")
plt.ylabel("値")
plt.legend()
plt.grid(True)
plt.show()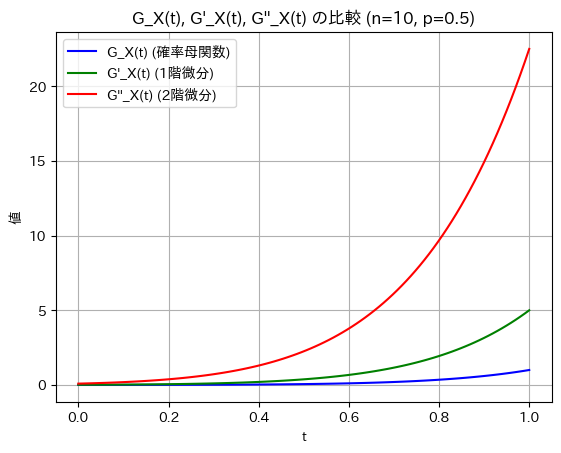
微分を重ねるごとにt=1付近での傾きが急になり大きな値を取っています。期待値や分散などの高次統計量に関連しているため、その値が大きくなっています。