負の二項分布
ポアソン-ガンマ混合分布は、負の二項分布になる
数式を使った計算
import sympy as sp
# 定義
k = sp.symbols('k', integer=True)
alpha, beta = sp.symbols('alpha beta', positive=True)
lambda_var = sp.symbols('lambda', positive=True)
# ポアソン分布の確率質量関数
poisson_pmf = (lambda_var**k * sp.exp(-lambda_var)) / sp.factorial(k)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha - 1) * sp.exp(-beta * lambda_var)
# 周辺分布の計算
marginal_distribution = sp.integrate(poisson_pmf * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
marginal_distribution
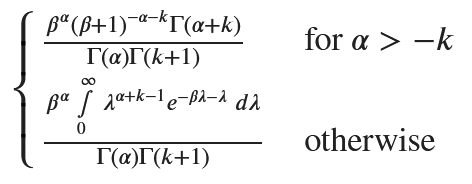
次式と同じなので、負の二項分布となる。

シミュレーションによる計算
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma, nbinom
# パラメータの設定
alpha = 3.0
beta = 2.0
sample_size = 10000
# ガンマ分布から λ を生成
lambda_samples = np.random.gamma(alpha, 1/beta, sample_size)
# 生成された λ を使ってポアソン分布から X を生成
poisson_samples = [np.random.poisson(lam) for lam in lambda_samples]
# 負の二項分布のパラメータを設定
r = alpha
p = beta / (beta + 1)
# 負の二項分布から理論的な確率質量関数を計算
x = np.arange(0, max(poisson_samples) + 1)
nbinom_pmf = nbinom.pmf(x, r, p)
# ヒストグラムの描画
plt.hist(poisson_samples, bins=np.arange(0, max(poisson_samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black', rwidth=0.8)
# 理論的な負の二項分布の確率質量関数をプロット
plt.plot(x, nbinom_pmf, 'r', linestyle='-', label='理論的な負の二項分布')
# グラフのタイトルとラベル
plt.title('ポアソン-ガンマ混合分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()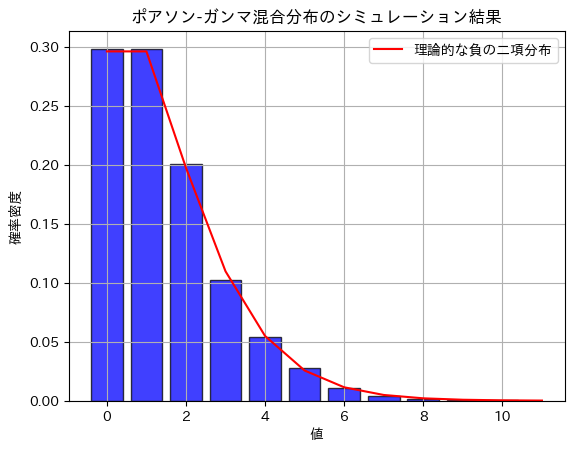
ガンマ分布
ガンマ分布の期待値と分散の導出
数式を使った計算
import sympy as sp
# 定義
lambda_var = sp.symbols('lambda')
alpha, beta = sp.symbols('alpha beta', positive=True)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha-1) * sp.exp(-beta * lambda_var)
# 期待値 E[Λ] の計算
expected_value = sp.integrate(lambda_var * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# E[Λ^2] の計算
expected_value_Lambda2 = sp.integrate(lambda_var**2 * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# 分散 V[Λ] の計算
variance = (expected_value_Lambda2 - expected_value**2).simplify()
# 結果を辞書形式で表示
{
"期待値 E[Λ]": expected_value,
"分散 V[Λ]": variance
}{'期待値 E[Λ]': alpha/beta, '分散 V[Λ]': alpha/beta**2}シミュレーションによる計算
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# サンプルサイズ
sample_size = 10000
# ガンマ分布に従う乱数を生成
samples = np.random.gamma(alpha, 1/beta, sample_size)
# 期待値と分散の計算
expected_value = np.mean(samples)
variance = np.var(samples)
# 結果の表示
print(f"期待値のシミュレーション結果: {expected_value}")
print(f"分散のシミュレーション結果: {variance}")
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なガンマ分布の確率密度関数をプロット
x = np.linspace(0, max(samples), 100)
gamma_pdf = gamma.pdf(x, alpha, scale=1/beta)
plt.plot(x, gamma_pdf, 'r', linestyle='-', label='理論的なガンマ分布')
# グラフのタイトルとラベル
plt.title('ガンマ分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()期待値のシミュレーション結果: 1.4947527551017439
分散のシミュレーション結果: 0.7452822182213243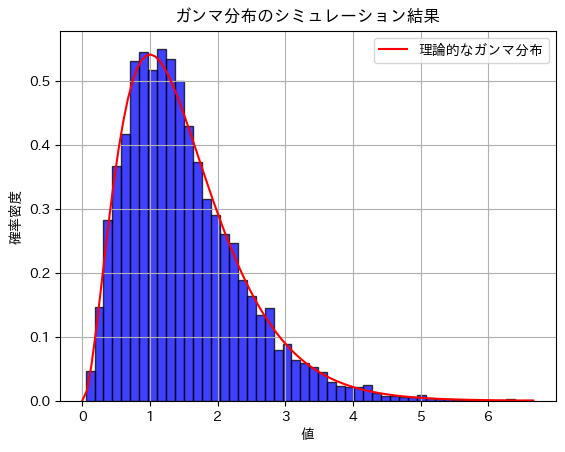
シミュレーションによる計算 (ガンマ分布に従う乱数生成関数をスクラッチで記述)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
def custom_exponential(beta):
# [0, 1) の一様乱数を生成
u = np.random.rand()
# 指数分布に従う乱数を生成
return -np.log(u) / beta
def custom_gamma(alpha, beta, sample_size):
samples = []
for _ in range(sample_size):
sample = sum(custom_exponential(beta) for _ in range(int(alpha)))
samples.append(sample)
return samples
# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# サンプルサイズ
sample_size = 10000
# カスタム関数を使ってガンマ分布に従う乱数を生成
samples = custom_gamma(alpha, beta, sample_size)
# 期待値と分散の計算
expected_value = np.mean(samples)
variance = np.var(samples)
# 理論値
theoretical_expected_value = alpha / beta
theoretical_variance = alpha / beta**2
# 結果の表示
print(f"シミュレーション結果 - 期待値: {expected_value}, 理論値: {theoretical_expected_value}")
print(f"シミュレーション結果 - 分散: {variance}, 理論値: {theoretical_variance}")
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なガンマ分布の確率密度関数をプロット
x = np.linspace(0, max(samples), 100)
gamma_pdf = gamma.pdf(x, alpha, scale=1/beta)
plt.plot(x, gamma_pdf, 'r', linestyle='-', label='理論的なガンマ分布')
# グラフのタイトルとラベル
plt.title('ガンマ分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()
シミュレーション結果 - 期待値: 1.4966126702823181, 理論値: 1.5
シミュレーション結果 - 分散: 0.7242038142114708, 理論値: 0.75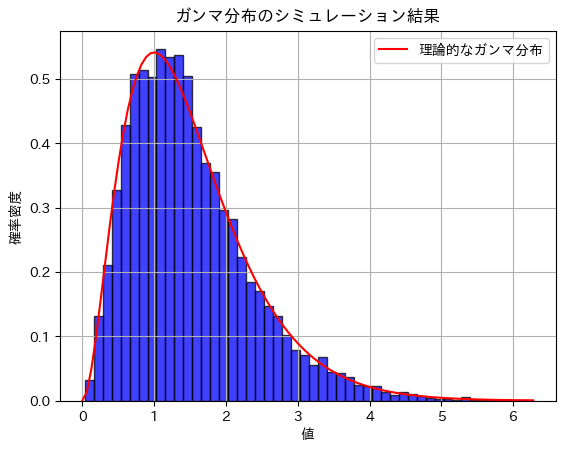
ポアソン分布
ポアソン分布の期待値と分散の導出
数式を使った計算
import sympy as sp
# 定義
k = sp.symbols('k')
lambda_param = sp.symbols('lambda')
# ポアソン分布の確率関数
poisson_pmf = (lambda_param**k * sp.exp(-lambda_param)) / sp.factorial(k)
# 期待値 E[X] の計算
expected_value = sp.summation(k * poisson_pmf, (k, 0, sp.oo)).simplify()
# E[X^2] の計算
expected_value_X2 = sp.summation(k**2 * poisson_pmf, (k, 0, sp.oo)).simplify()
# 分散 V[X] の計算
variance = (expected_value_X2 - expected_value**2).simplify()
# 結果を表示
{
"期待値 E[X]": expected_value,
"分散 V[X]": variance
}{'期待値 E[X]': lambda, '分散 V[X]': lambda}シミュレーションによる計算
import numpy as np
# パラメータ λ の設定
lambda_param = 5
# シミュレーションの回数
num_simulations = 10000
# 各シミュレーションで生成するサンプルの数
sample_size = 1000
# シミュレーション結果の保存用
expected_values = []
variances = []
for _ in range(num_simulations):
# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)
# 期待値を計算
expected_values.append(np.mean(samples))
# 分散を計算
variances.append(np.var(samples))
# シミュレーション結果の平均を計算
average_expected_value = np.mean(expected_values)
average_variance = np.mean(variances)
print(f"期待値のシミュレーション結果: {average_expected_value}")
print(f"分散のシミュレーション結果: {average_variance}")期待値のシミュレーション結果: 4.999602
分散のシミュレーション結果: 4.9992533574プロット
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
# パラメータ λ の設定
lambda_param = 5
# サンプルサイズ
sample_size = 10000
# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)
# ヒストグラムの描画
plt.hist(samples, bins=np.arange(0, max(samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なポアソン分布の確率質量関数をプロット
x = np.arange(0, max(samples) + 1)
poisson_pmf = (lambda_param**x * np.exp(-lambda_param)) / factorial(x)
plt.plot(x, poisson_pmf, 'r', marker='o', linestyle='-', label='理論的なポアソン分布')
# グラフのタイトルとラベル
plt.title('ポアソン分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()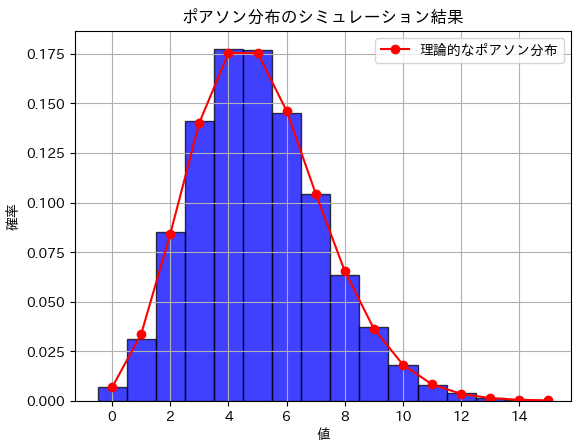
シミュレーションによる計算 (ポアソン分布に従う乱数生成関数をスクラッチで記述)
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
def custom_poisson(lambda_param, sample_size):
samples = []
for _ in range(sample_size):
k = 0
p = np.exp(-lambda_param)
sum_p = p
u = np.random.rand()
while u > sum_p:
k += 1
p *= lambda_param / k
sum_p += p
samples.append(k)
return samples
# パラメータ λ の設定
lambda_param = 5
# サンプルサイズ
sample_size = 10000
# カスタム関数を使ってポアソン分布に従う乱数を生成
samples = custom_poisson(lambda_param, sample_size)
# ヒストグラムの描画
plt.hist(samples, bins=np.arange(0, max(samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なポアソン分布の確率質量関数をプロット
x = np.arange(0, max(samples) + 1)
poisson_pmf = (lambda_param**x * np.exp(-lambda_param)) / factorial(x)
plt.plot(x, poisson_pmf, 'r', marker='o', linestyle='-', label='理論的なポアソン分布')
# グラフのタイトルとラベル
plt.title('ポアソン分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()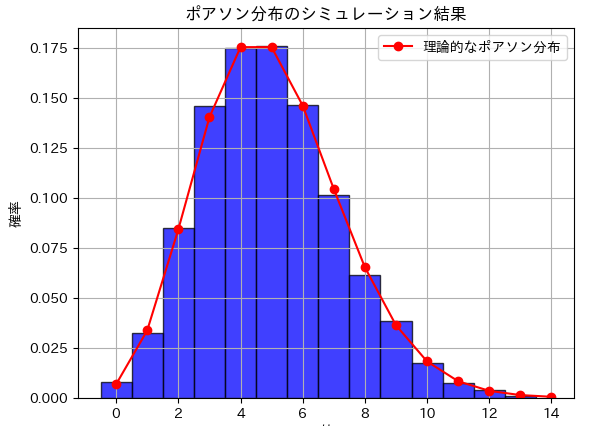
乱数生成のプロセス
- 初期化:
kを 0 に設定します(ポアソン分布の乱数)。pを exp(−λ)に設定します(初期確率)。sum_pをpに設定します。uを [0, 1) の一様乱数として生成します。
- 累積確率と乱数の比較:
uがsum_pより大きい間、以下のステップを繰り返します。kを増加させます。pを更新し、累積確率sum_pに追加します。
- サンプル追加:
- ループが終了すると、
kをsamplesリストに追加します。
- ループが終了すると、
この方法により、ポアソン分布に従う乱数を自作関数で生成することができます。他に質問があれば、お知らせください。
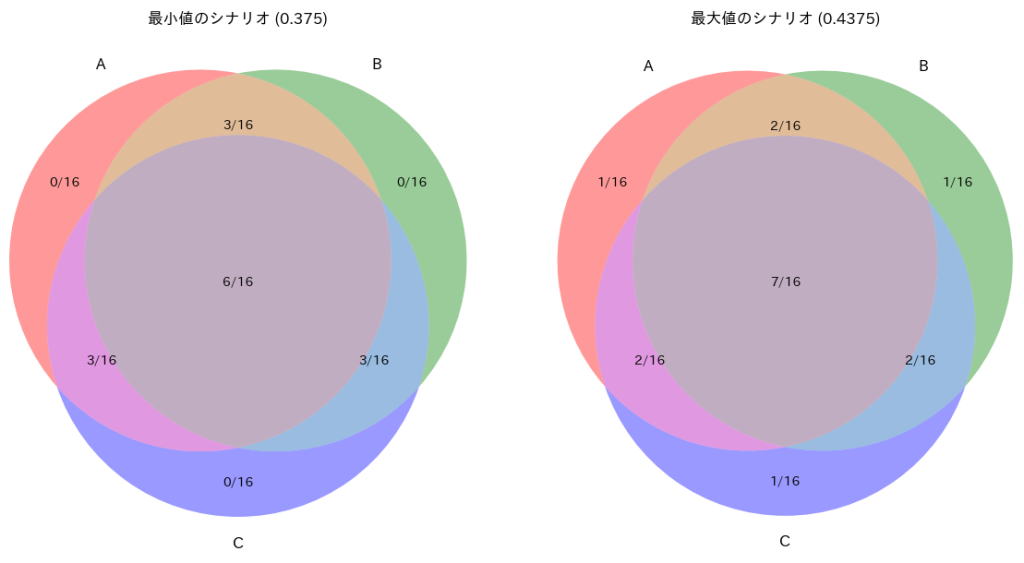
確率空間の事象 A,B,CのP(A∩B∩C)のとり得る範囲
問
確率空間の事象 A,B,C の確率がそれぞれ P(A) = P(B) = P(C) = ![]()
かつ P(A∩B)=P(A)P(B) , P(A∩C)=P(A)P(C) , P(B∩C)=P(B)P(C)
のとき、P(A∩B∩C)のとり得る範囲は?
解き方
A、B、Cのベン図が持つ8個のエリアに対して16個の点を配置し、特定の確率条件を満たす事象の組み合わせをシミュレーションによって求める。事象A、B、Cの個別確率およびそれらの共通部分の確率を基に、各エリアに属する点数の全ての可能な組み合わせを探索する。各組み合わせについて計算を行い、条件を満たす場合はその組み合わせをリストに追加し、最小値と最大値を更新する。最終的に、条件を満たす最小および最大の値を特定し、それぞれの点数の組み合わせを明らかにする。結果として、条件を満たす最小値と最大値に対応する具体的な点数の配分が得られる。
コード
# 定数
total_points = 16
PA = 3 / 4
PB = 3 / 4
PC = 3 / 4
PAB = 9 / 16
PAC = 9 / 16
PBC = 9 / 16
# 結果を格納するリスト
valid_probabilities = []
# 最小値と最大値を取るときの組み合わせを格納する変数
min_combination = None
max_combination = None
min_value = float('inf')
max_value = float('-inf')
# 各エリアの点数の範囲を狭める
for n1 in range(total_points // 3 + 1):
for n2 in range((total_points - 3 * n1) // 3 + 1):
for n3 in range(total_points - 3 * n1 - 3 * n2 + 1):
n4 = total_points - 3 * n1 - 3 * n2 - n3
if n4 < 0:
continue
calc_PA = (n1 + 2 * n2 + n4) / total_points
calc_PB = (n1 + 2 * n2 + n4) / total_points
calc_PC = (n1 + 2 * n2 + n4) / total_points
calc_PAB = (n2 + n4) / total_points
calc_PAC = (n2 + n4) / total_points
calc_PBC = (n2 + n4) / total_points
# 条件を満たすか確認
if (abs(calc_PA - PA) < 1e-9 and
abs(calc_PB - PB) < 1e-9 and
abs(calc_PC - PC) < 1e-9 and
abs(calc_PAB - PAB) < 1e-9 and
abs(calc_PAC - PAC) < 1e-9 and
abs(calc_PBC - PBC) < 1e-9):
current_PABC = n4 / total_points
valid_probabilities.append(current_PABC)
if current_PABC < min_value:
min_value = current_PABC
min_combination = (n1, n2, n3, n4)
if current_PABC > max_value:
max_value = current_PABC
max_combination = (n1, n2, n3, n4)
# 最小値と最大値を表示
min_PABC = min_value if valid_probabilities else None
max_PABC = max_value if valid_probabilities else None
# 結果の表示
print(f"最小値: {min_PABC}")
print(f"最大値: {max_PABC}")
print(f"最小値を取るときのN1, N2, N3, N4: {min_combination}")
print(f"最大値を取るときのN1, N2, N3, N4: {max_combination}")
最小値: 0.375
最大値: 0.4375
最小値を取るときのN1, N2, N3, N4: (0, 3, 1, 6)
最大値を取るときのN1, N2, N3, N4: (1, 2, 0, 7)