独立な指数分布に従う2変数の和の確率
指数分布の和はガンマ分布に従います。
X1,X2は互いに独立でパラメータλを持つ指数分布に従います。
U=X1+X2とします
数式を使ってUの確率密度関数を求めます。
import sympy as sp
# 変数の定義
x, u, lambda_value = sp.symbols('x u lambda', positive=True, real=True)
# 指数分布の確率密度関数 (PDF) f(x)
f_x = lambda_value * sp.exp(-lambda_value * x)
# 畳み込み積分を計算して、g(u) = f(x) * f(u - x) の形式にする
g_u = sp.integrate(f_x * lambda_value * sp.exp(-lambda_value * (u - x)), (x, 0, u))
# 簡略化
g_u_simplified = sp.simplify(g_u)
# 結果の表示
display(g_u_simplified)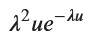
求まりました。
X1 (X2)と、Uの確率密度関数を重ねて描画してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2 の範囲
# X1, X2 の指数分布の確率密度関数 (PDF) - 同じなので1つにまとめる
pdf_X1_X2 = lambda_value * np.exp(-lambda_value * x_range)
# U = X1 + X2 は形状パラメータk=2、スケールパラメータθ=1/λのガンマ分布
u_range = np.linspace(0, 10, 1000)
pdf_U = gamma.pdf(u_range, a=2, scale=1/lambda_value)
# グラフのプロット
plt.figure(figsize=(8, 6))
# X1 (X2) の指数分布の描画
plt.plot(x_range, pdf_X1_X2, label='X1 (X2) (指数分布)', color='blue', linestyle='--')
# U のガンマ分布の描画
plt.plot(u_range, pdf_U, label='U = X1 + X2 (ガンマ分布)', color='red')
# グラフの装飾
plt.title('X1 (X2) と U の確率密度関数の比較')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.show()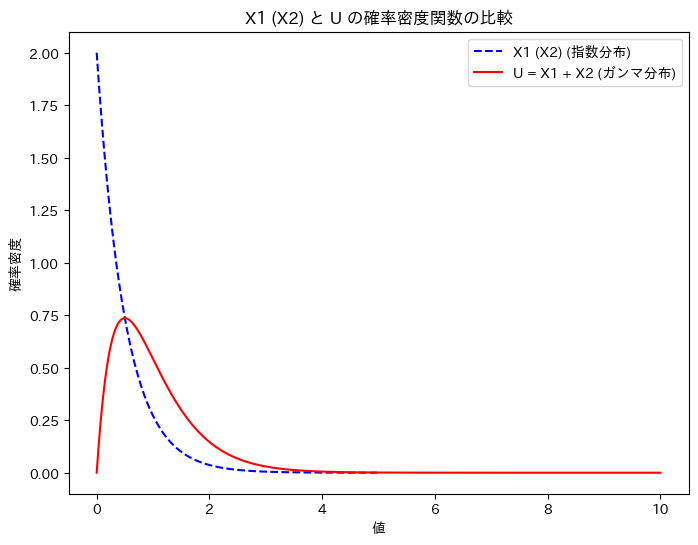
グラフの形状から、U = X1 + X2の関係は想像しづらいですね。
ガンマ分布の形状パラメータを1~2に変化させて、X1 (X2)からUへの変化を確認します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2, U の範囲を0~5に設定
# ガンマ分布の形状パラメータを1から2まで0.1ずつ変化させる
shape_params = np.arange(1, 2.1, 0.1) # 1から2までの形状パラメータを0.1ステップで変化
# グラフのプロット
plt.figure(figsize=(8, 6))
# 形状パラメータが1から2に変化するガンマ分布の描画
for k in shape_params:
gamma_pdf = gamma.pdf(x_range, a=k, scale=1/lambda_value)
plt.plot(x_range, gamma_pdf, label=f'形状パラメータ k={k:.1f}')
# X1 (X2) の指数分布の描画 - 同じなので1つにまとめる
pdf_X1_X2 = lambda_value * np.exp(-lambda_value * x_range)
plt.plot(x_range, pdf_X1_X2, label='X1 (X2) (指数分布)', color='blue', linestyle='--')
# グラフの装飾
plt.title('指数分布からガンマ分布への変化 (形状パラメータの0.1ステップ変化)')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.show()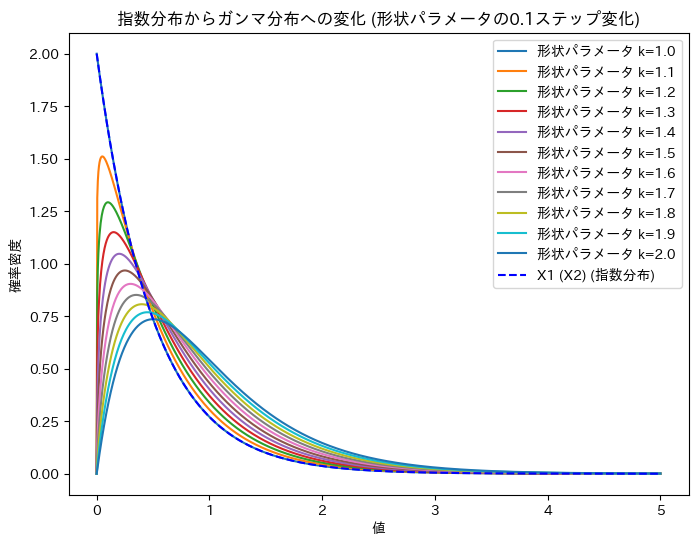
X1 (X2)からUへの変化が可視化できました。
次に、X1 (X2)と、Uの累積分布関数を重ねて描画してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon, gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2 の範囲
# X1, X2 の指数分布の累積分布関数 (CDF) - 同じなので1つにまとめる
cdf_X1_X2 = expon.cdf(x_range, scale=1/lambda_value)
# U = X1 + X2 は形状パラメータk=2、スケールパラメータθ=1/λのガンマ分布
u_range = np.linspace(0, 10, 1000)
cdf_U = gamma.cdf(u_range, a=2, scale=1/lambda_value)
# グラフのプロット
plt.figure(figsize=(8, 6))
# X1 (X2) の指数分布のCDFの描画
plt.plot(x_range, cdf_X1_X2, label='X1 (X2) (指数分布 CDF)', color='blue', linestyle='--')
# U のガンマ分布のCDFの描画
plt.plot(u_range, cdf_U, label='U = X1 + X2 (ガンマ分布 CDF)', color='red')
# グラフの装飾
plt.title('X1 (X2) と U の累積分布関数 (CDF) の比較')
plt.xlabel('値')
plt.ylabel('累積確率')
plt.legend()
# グラフの表示
plt.show()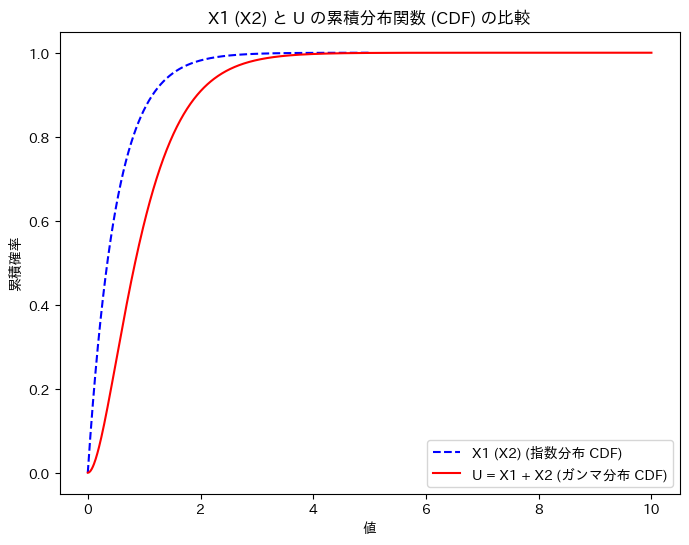
グラフの形状から、U = X1 + X2の関係を想像しやすくなりました。
豆の非復元抽出
豆の非復元抽出は超幾何分布になる
豆の実験の概要
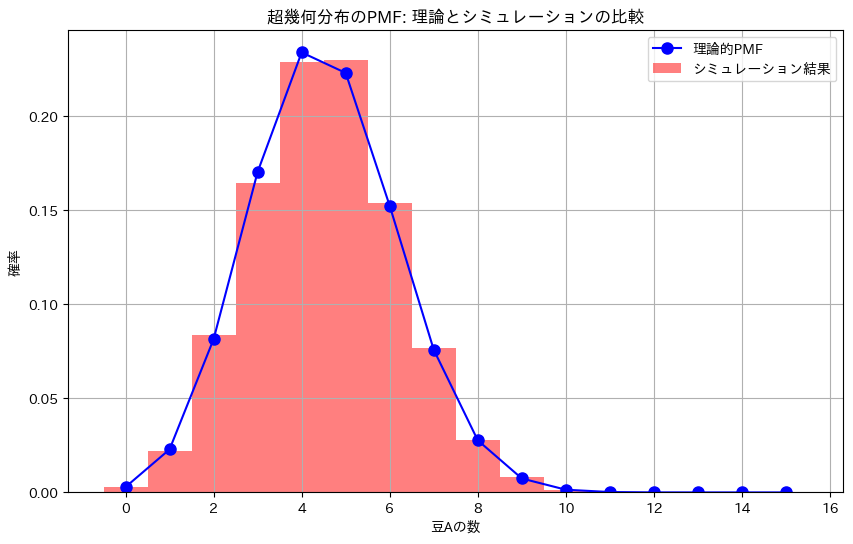
この実験は、100個の豆が入った袋の中から無作為に15個の豆を取り出し、その中に含まれる特定の種類の豆(豆A)の数を調べるシミュレーションを通じて、超幾何分布がどのように現実の状況を表現するかを確認するものです。
実験の設定:
- 袋の中の豆の総数: 100個
- 豆Aの数: 30個
- 豆Bの数: 70個
- 取り出す豆の数: 15個
実験の手順:
- 袋に入っている100個の豆のうち、30個が豆Aであり、残り70個が豆Bであるとします。
- 袋から無作為に15個の豆を非復元で抽出し、その中に含まれる豆Aの数を数えます。
- この抽出操作を10000回繰り返し、各回で得られた豆Aの数を記録します。
- 記録されたデータを基に、豆Aの数の分布をヒストグラムとして描画し、理論的に計算された超幾何分布と比較します。
実験の目的:
- この実験の目的は、理論的な超幾何分布が、豆を無作為に非復元抽出した際の豆Aの数の分布をどの程度正確に表現できるかを確認することです。
- 結果として得られるシミュレーションの分布が、理論的な超幾何分布とよく一致することが期待されます。これにより、超幾何分布が現実の非復元抽出を扱う際に有効であることが示されます。
結果の分析:
- シミュレーションの結果と理論的な超幾何分布を比較することで、両者の一致度を確認します。
- この実験は、非復元抽出のシナリオで生じる確率分布が、理論的な超幾何分布に従うことを実証的に示すものです。
シミュレーションによる計算
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import hypergeom
# パラメータの設定
M = 100 # 全体の豆の数
N_A = 30 # 豆Aの数
n = 15 # 抽出する豆の数
x_values = np.arange(0, n+1) # 可能な豆Aの数
# 理論的な超幾何分布のPMFを計算
rv = hypergeom(M, N_A, n)
pmf_theoretical = rv.pmf(x_values)
# 数値シミュレーションの設定
n_simulations = 10000 # シミュレーション回数
simulated_counts = []
# シミュレーションの実行
for _ in range(n_simulations):
# 袋の中の豆を表すリスト(1が豆A、0が豆B)
bag = np.array([1]*N_A + [0]*(M - N_A))
# 無作為に15個抽出
sample = np.random.choice(bag, size=n, replace=False)
# 抽出した中の豆Aの数をカウント
count_A = np.sum(sample)
simulated_counts.append(count_A)
# シミュレーションから得られたPMFを計算
pmf_simulated, bins = np.histogram(simulated_counts, bins=np.arange(-0.5, n+1.5, 1), density=True)
# グラフの描画
plt.figure(figsize=(10, 6))
# 理論的なPMFの描画
plt.plot(x_values, pmf_theoretical, 'bo-', label='理論的PMF', markersize=8)
# シミュレーション結果をヒストグラムとして描画
plt.hist(simulated_counts, bins=np.arange(-0.5, n+1.5, 1), density=True, alpha=0.5, color='red', label='シミュレーション結果')
# グラフの設定
plt.xlabel('豆Aの数')
plt.ylabel('確率')
plt.title('超幾何分布のPMF: 理論とシミュレーションの比較')
plt.legend()
plt.grid(True)
plt.show()