二項分布と超幾何分布
二項分布
- 抽出方法: 復元抽出
- 試行の独立性: 各試行は独立
- 確率: 各試行で成功確率は一定
超幾何分布
- 抽出方法: 非復元抽出
- 試行の独立性: 各試行は独立していない
- 確率: 各試行で成功確率が変化
グラフの比較
今回の実験では、二項分布と超幾何分布の違いを視覚的に比較します。二項分布は、復元抽出を行う場合に適用され、各試行が独立しており、成功確率が一定です。一方、超幾何分布は、非復元抽出を行う場合に適用され、試行ごとに成功確率が変化します。実験では、母集団のサイズ、成功対象の数、抽出回数を変え、それぞれのグラフを描画します。特に、サンプルサイズが大きい場合や母集団が小さい場合など、分布の形状に顕著な違いが現れる条件に注目して比較を行います。これにより、抽出方法による分布の違いを視覚的に確認し、二項分布と超幾何分布の特性を理解します。
復元抽出と非復元抽出の比較(広範囲のパラメータ設定)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# パラメータ比を一定に保ったグラフを作成
M_values = [50, 150, 250, 350, 450]
N_A_values = [15, 45, 75, 105, 135] # M の 30%
n_values = [7, 22, 37, 52, 67] # M の 15%
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(5, 1, figsize=(10, 30))
# 異なるパラメータ設定でグラフを描画
for i in range(5):
plot_comparison(M=M_values[i], N_A=N_A_values[i], n=n_values[i], ax=axs[i])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()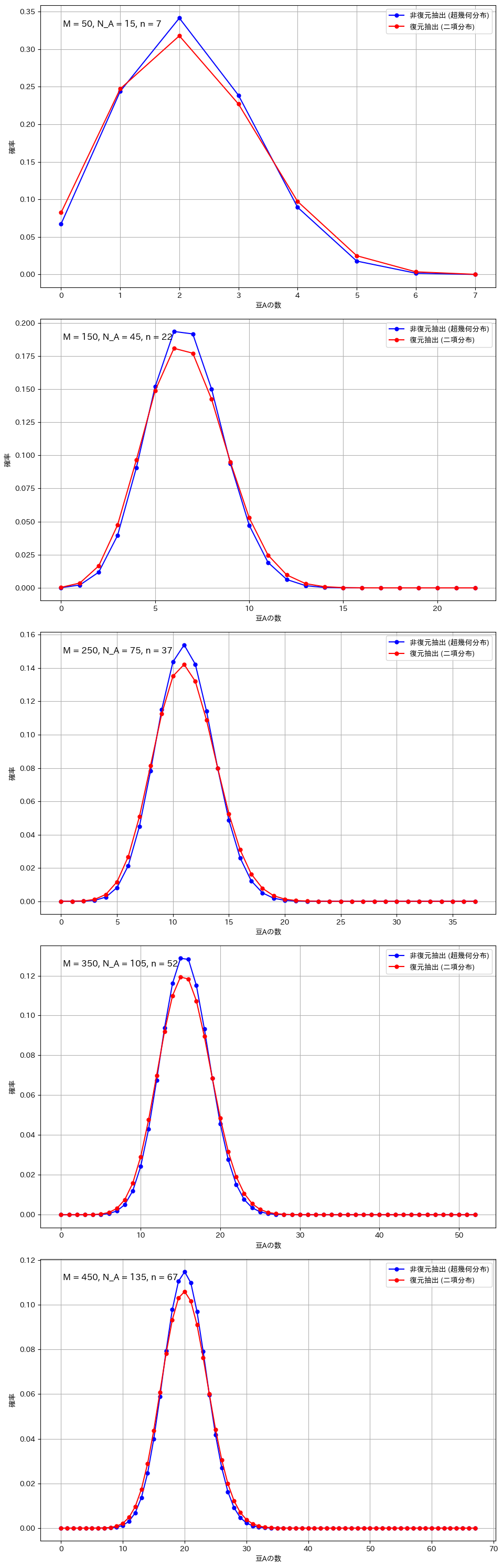
復元抽出と非復元抽出の比較(顕著な違いが現れる条件)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(3, 1, figsize=(10, 18)) # 高さを調整
# 条件1: サンプルサイズが大きい場合
plot_comparison(M=100, N_A=30, n=80, ax=axs[0])
# 条件2: 全体のサイズが小さい場合
plot_comparison(M=20, N_A=6, n=15, ax=axs[1])
# 条件3: 極端な割合の場合
plot_comparison(M=100, N_A=90, n=30, ax=axs[2])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()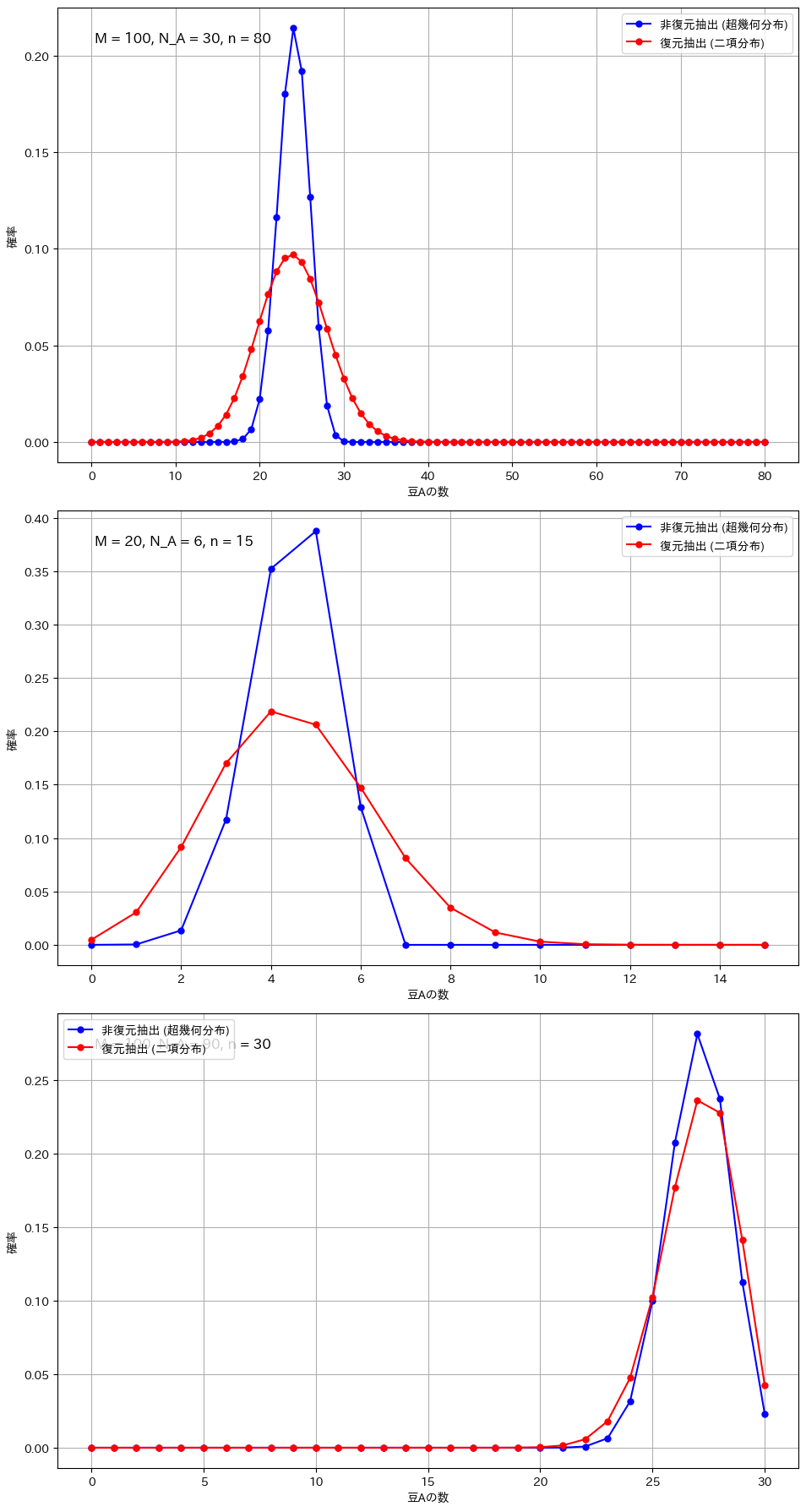
考察
二項分布と超幾何分布の違いが顕著になるのは、サンプルサイズが全体に対して大きい場合や、母集団が小さい場合です。例えば、全体の豆の数が100個で80個を抽出する場合や、母集団が20個でそのうち15個を抽出する場合、非復元抽出では次の試行に与える影響が大きくなり、復元抽出との差が明確に現れます。また、成功確率が極端に高いか低い場合も、非復元抽出の影響で分布が変わりやすくなります。一方、サンプルサイズが小さい場合や母集団が非常に大きい場合には、各抽出の影響が少なく、二項分布と超幾何分布の違いは目立たなくなります。
混合ガウスモデルによる観測データの分布特性推定
概要:
本実験では、観測データが複数の異なる分布の混合によって生成されている可能性を考慮し、その分布特性を推定する手法を検証する。具体的には、2つの正規分布を混合したデータを生成し、EMアルゴリズムを用いてその混合ガウスモデルをフィッティングする。実験の結果、生成されたデータの背後にある各分布の平均、標準偏差、および混合割合を高精度に推定できることを確認した。本手法は、複雑な観測データに対する分布特性の解析やデータの要因分解に有効である。
2つの成分
import numpy as np
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 1. データ生成: 混合正規分布から乱数を生成
np.random.seed(0)
n_samples = 1000
# 2つの正規分布のパラメータ設定
mean1, std1 = 0, 1 # 正規分布1
mean2, std2 = 5, 1.5 # 正規分布2
weight1, weight2 = 0.4, 0.6 # 混合割合
# 2つの分布からデータ生成
data1 = np.random.normal(mean1, std1, int(weight1 * n_samples))
data2 = np.random.normal(mean2, std2, int(weight2 * n_samples))
# 混合データの作成
data = np.hstack([data1, data2])
np.random.shuffle(data)
# 2. 混合モデルの構築とフィッティング (EMアルゴリズムを使用)
gmm = GaussianMixture(n_components=2, random_state=0)
gmm.fit(data.reshape(-1, 1))
# 推定されたパラメータ
means = gmm.means_.flatten()
std_devs = np.sqrt(gmm.covariances_).flatten()
weights = gmm.weights_
print("推定された平均:", means)
print("推定された標準偏差:", std_devs)
print("推定された混合割合:", weights)
# 3. 結果のプロット
x = np.linspace(-3, 10, 1000)
pdf1 = weights[0] * (1 / (std_devs[0] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[0])**2 / (2 * std_devs[0]**2)))
pdf2 = weights[1] * (1 / (std_devs[1] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[1])**2 / (2 * std_devs[1]**2)))
plt.hist(data, bins=30, density=True, alpha=0.5, color='gray', label='データのヒストグラム')
plt.plot(x, pdf1 + pdf2, 'r-', lw=2, label='フィッティングされたモデル')
plt.plot(x, pdf1, 'b--', lw=2, label='成分 1')
plt.plot(x, pdf2, 'g--', lw=2, label='成分 2')
plt.title('データとフィッティングされた混合ガウスモデル')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()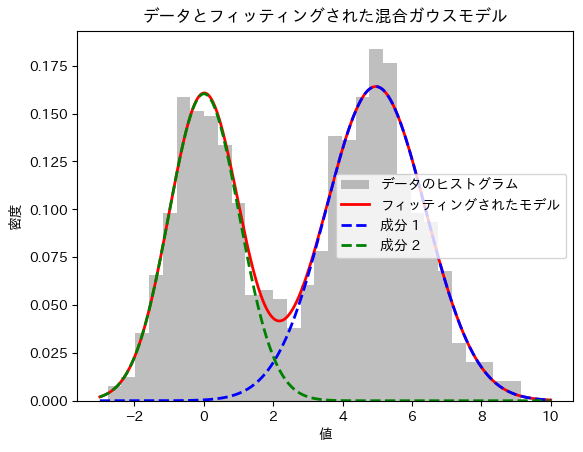
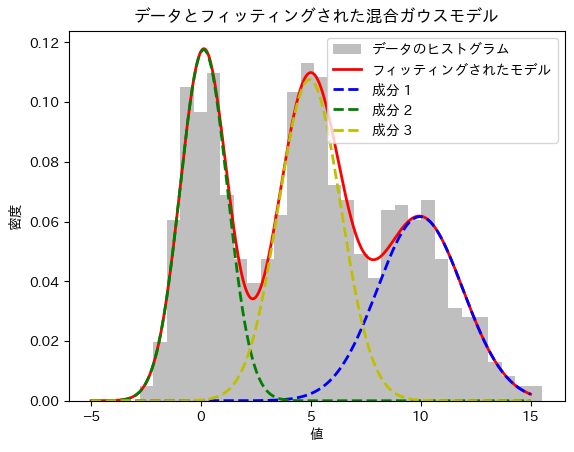
3つの成分
import numpy as np
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 1. データ生成: 混合正規分布から乱数を生成
np.random.seed(0)
n_samples = 1000
# 3つの正規分布のパラメータ設定
mean1, std1 = 0, 1 # 正規分布1
mean2, std2 = 5, 1.5 # 正規分布2
mean3, std3 = 10, 2 # 正規分布3
weight1, weight2, weight3 = 0.3, 0.4, 0.3 # 混合割合
# 3つの分布からデータ生成
data1 = np.random.normal(mean1, std1, int(weight1 * n_samples))
data2 = np.random.normal(mean2, std2, int(weight2 * n_samples))
data3 = np.random.normal(mean3, std3, int(weight3 * n_samples))
# 混合データの作成
data = np.hstack([data1, data2, data3])
np.random.shuffle(data)
# 2. 混合モデルの構築とフィッティング (EMアルゴリズムを使用)
gmm = GaussianMixture(n_components=3, random_state=0)
gmm.fit(data.reshape(-1, 1))
# 推定されたパラメータ
means = gmm.means_.flatten()
std_devs = np.sqrt(gmm.covariances_).flatten()
weights = gmm.weights_
print("推定された平均:", means)
print("推定された標準偏差:", std_devs)
print("推定された混合割合:", weights)
# 3. 結果のプロット
x = np.linspace(-5, 15, 1000)
pdf1 = weights[0] * (1 / (std_devs[0] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[0])**2 / (2 * std_devs[0]**2)))
pdf2 = weights[1] * (1 / (std_devs[1] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[1])**2 / (2 * std_devs[1]**2)))
pdf3 = weights[2] * (1 / (std_devs[2] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[2])**2 / (2 * std_devs[2]**2)))
plt.hist(data, bins=30, density=True, alpha=0.5, color='gray', label='データのヒストグラム')
plt.plot(x, pdf1 + pdf2 + pdf3, 'r-', lw=2, label='フィッティングされたモデル')
plt.plot(x, pdf1, 'b--', lw=2, label='成分 1')
plt.plot(x, pdf2, 'g--', lw=2, label='成分 2')
plt.plot(x, pdf3, 'y--', lw=2, label='成分 3')
plt.title('データとフィッティングされた混合ガウスモデル')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()