ホーム » 分布 » ポアソン分布 » ポアソン分布

和みLab

アーカイブ

カテゴリー

ポアソン分布

投稿者: in ポアソン分布 投稿日:

ポアソン分布の期待値と分散の導出

数式を使った計算

import sympy as sp

# 定義
k = sp.symbols('k')
lambda_param = sp.symbols('lambda')

# ポアソン分布の確率関数
poisson_pmf = (lambda_param**k * sp.exp(-lambda_param)) / sp.factorial(k)

# 期待値 E[X] の計算
expected_value = sp.summation(k * poisson_pmf, (k, 0, sp.oo)).simplify()

# E[X^2] の計算
expected_value_X2 = sp.summation(k**2 * poisson_pmf, (k, 0, sp.oo)).simplify()

# 分散 V[X] の計算
variance = (expected_value_X2 - expected_value**2).simplify()

# 結果を表示
{
    "期待値 E[X]": expected_value,
    "分散 V[X]": variance
}
{'期待値 E[X]': lambda, '分散 V[X]': lambda}

シミュレーションによる計算

import numpy as np

# パラメータ λ の設定
lambda_param = 5
# シミュレーションの回数
num_simulations = 10000
# 各シミュレーションで生成するサンプルの数
sample_size = 1000

# シミュレーション結果の保存用
expected_values = []
variances = []

for _ in range(num_simulations):
    # ポアソン分布に従う乱数を生成
    samples = np.random.poisson(lambda_param, sample_size)
    # 期待値を計算
    expected_values.append(np.mean(samples))
    # 分散を計算
    variances.append(np.var(samples))

# シミュレーション結果の平均を計算
average_expected_value = np.mean(expected_values)
average_variance = np.mean(variances)

print(f"期待値のシミュレーション結果: {average_expected_value}")
print(f"分散のシミュレーション結果: {average_variance}")
期待値のシミュレーション結果: 4.999602
分散のシミュレーション結果: 4.9992533574

プロット

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial

# パラメータ λ の設定
lambda_param = 5
# サンプルサイズ
sample_size = 10000

# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)

# ヒストグラムの描画
plt.hist(samples, bins=np.arange(0, max(samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black')

# 理論的なポアソン分布の確率質量関数をプロット
x = np.arange(0, max(samples) + 1)
poisson_pmf = (lambda_param**x * np.exp(-lambda_param)) / factorial(x)
plt.plot(x, poisson_pmf, 'r', marker='o', linestyle='-', label='理論的なポアソン分布')

# グラフのタイトルとラベル
plt.title('ポアソン分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率')
plt.legend()

# グラフの表示
plt.grid(True)
plt.show()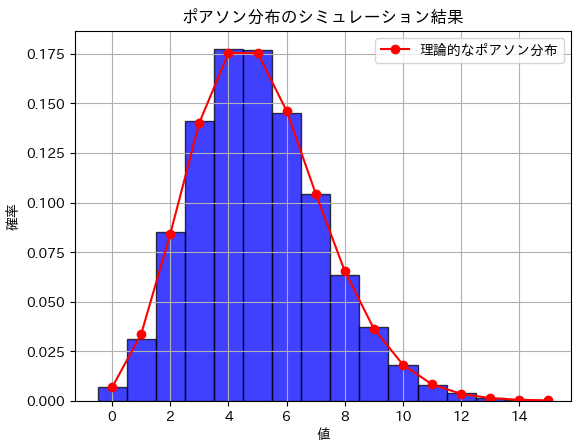

シミュレーションによる計算　（ポアソン分布に従う乱数生成関数をスクラッチで記述）

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial

def custom_poisson(lambda_param, sample_size):
    samples = []
    for _ in range(sample_size):
        k = 0
        p = np.exp(-lambda_param)
        sum_p = p
        u = np.random.rand()
        while u > sum_p:
            k += 1
            p *= lambda_param / k
            sum_p += p
        samples.append(k)
    return samples

# パラメータ λ の設定
lambda_param = 5
# サンプルサイズ
sample_size = 10000

# カスタム関数を使ってポアソン分布に従う乱数を生成
samples = custom_poisson(lambda_param, sample_size)

# ヒストグラムの描画
plt.hist(samples, bins=np.arange(0, max(samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black')

# 理論的なポアソン分布の確率質量関数をプロット
x = np.arange(0, max(samples) + 1)
poisson_pmf = (lambda_param**x * np.exp(-lambda_param)) / factorial(x)
plt.plot(x, poisson_pmf, 'r', marker='o', linestyle='-', label='理論的なポアソン分布')

# グラフのタイトルとラベル
plt.title('ポアソン分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率')
plt.legend()

# グラフの表示
plt.grid(True)
plt.show()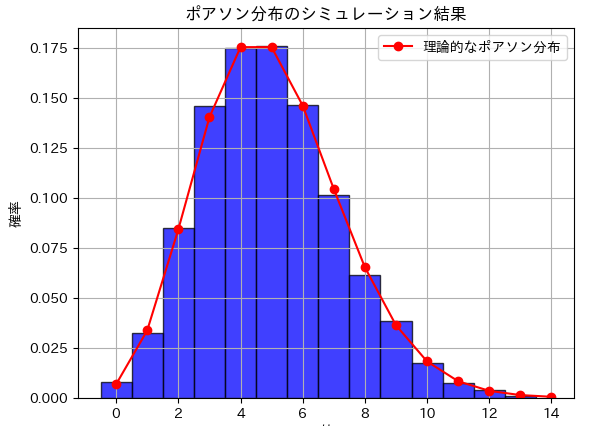

乱数生成のプロセス

  1. 初期化:
    • k を 0 に設定します（ポアソン分布の乱数）。
    • p を exp⁡(−λ)に設定します（初期確率）。
    • sum_p を p に設定します。
    • u を [0, 1) の一様乱数として生成します。
  2. 累積確率と乱数の比較:
    • u が sum_p より大きい間、以下のステップを繰り返します。
      • k を増加させます。
      • p を更新し、累積確率 sum_p に追加します。
  3. サンプル追加:
    • ループが終了すると、k を samples リストに追加します。

この方法により、ポアソン分布に従う乱数を自作関数で生成することができます。他に質問があれば、お知らせください。