負の二項分布
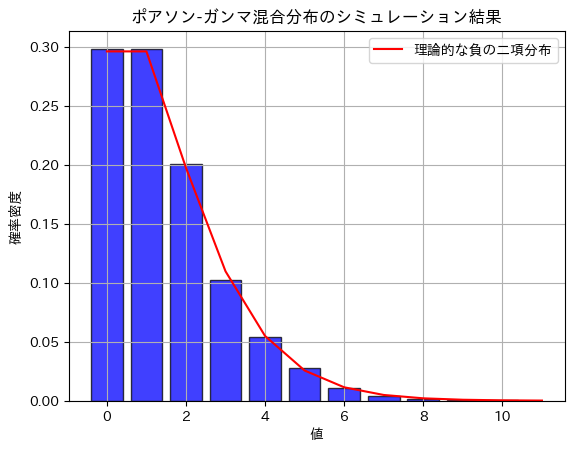
ポアソン-ガンマ混合分布は、負の二項分布になる
数式を使った計算
import sympy as sp
# 定義
k = sp.symbols('k', integer=True)
alpha, beta = sp.symbols('alpha beta', positive=True)
lambda_var = sp.symbols('lambda', positive=True)
# ポアソン分布の確率質量関数
poisson_pmf = (lambda_var**k * sp.exp(-lambda_var)) / sp.factorial(k)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha - 1) * sp.exp(-beta * lambda_var)
# 周辺分布の計算
marginal_distribution = sp.integrate(poisson_pmf * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
marginal_distribution
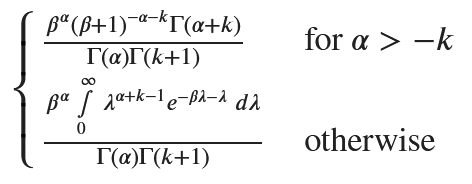
次式と同じなので、負の二項分布となる。

シミュレーションによる計算
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma, nbinom
# パラメータの設定
alpha = 3.0
beta = 2.0
sample_size = 10000
# ガンマ分布から λ を生成
lambda_samples = np.random.gamma(alpha, 1/beta, sample_size)
# 生成された λ を使ってポアソン分布から X を生成
poisson_samples = [np.random.poisson(lam) for lam in lambda_samples]
# 負の二項分布のパラメータを設定
r = alpha
p = beta / (beta + 1)
# 負の二項分布から理論的な確率質量関数を計算
x = np.arange(0, max(poisson_samples) + 1)
nbinom_pmf = nbinom.pmf(x, r, p)
# ヒストグラムの描画
plt.hist(poisson_samples, bins=np.arange(0, max(poisson_samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black', rwidth=0.8)
# 理論的な負の二項分布の確率質量関数をプロット
plt.plot(x, nbinom_pmf, 'r', linestyle='-', label='理論的な負の二項分布')
# グラフのタイトルとラベル
plt.title('ポアソン-ガンマ混合分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()