ホーム » 事象と確率
「事象と確率」カテゴリーアーカイブ
確率空間の事象 A,B,CのP(A∩B∩C)のとり得る範囲
問
確率空間の事象 A,B,C の確率がそれぞれ P(A) = P(B) = P(C) = ![]()
かつ P(A∩B)=P(A)P(B) , P(A∩C)=P(A)P(C) , P(B∩C)=P(B)P(C)
のとき、P(A∩B∩C)のとり得る範囲は?
解き方
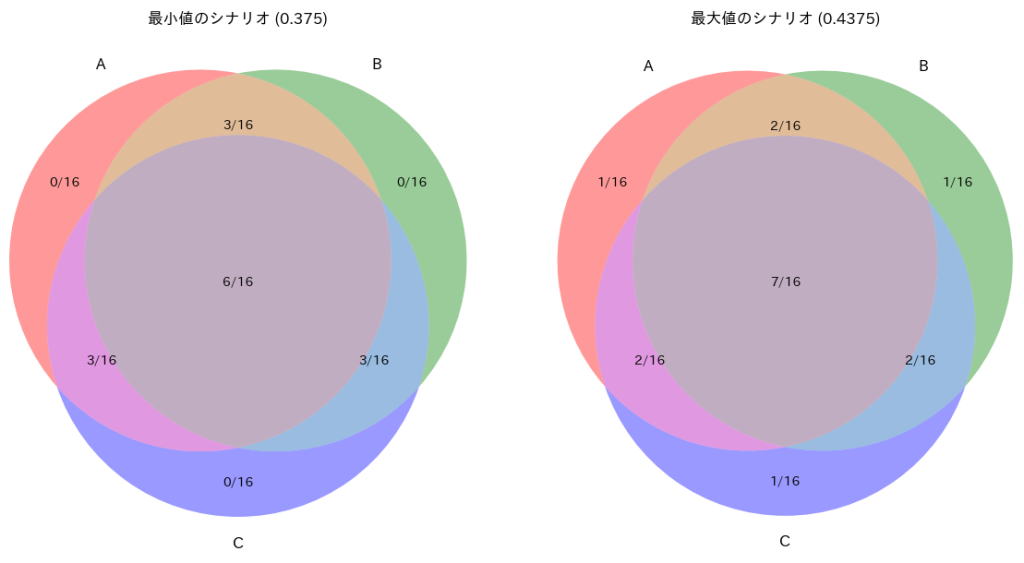
A、B、Cのベン図が持つ8個のエリアに対して16個の点を配置し、特定の確率条件を満たす事象の組み合わせをシミュレーションによって求める。事象A、B、Cの個別確率およびそれらの共通部分の確率を基に、各エリアに属する点数の全ての可能な組み合わせを探索する。各組み合わせについて計算を行い、条件を満たす場合はその組み合わせをリストに追加し、最小値と最大値を更新する。最終的に、条件を満たす最小および最大の値を特定し、それぞれの点数の組み合わせを明らかにする。結果として、条件を満たす最小値と最大値に対応する具体的な点数の配分が得られる。
コード
# 定数
total_points = 16
PA = 3 / 4
PB = 3 / 4
PC = 3 / 4
PAB = 9 / 16
PAC = 9 / 16
PBC = 9 / 16
# 結果を格納するリスト
valid_probabilities = []
# 最小値と最大値を取るときの組み合わせを格納する変数
min_combination = None
max_combination = None
min_value = float('inf')
max_value = float('-inf')
# 各エリアの点数の範囲を狭める
for n1 in range(total_points // 3 + 1):
for n2 in range((total_points - 3 * n1) // 3 + 1):
for n3 in range(total_points - 3 * n1 - 3 * n2 + 1):
n4 = total_points - 3 * n1 - 3 * n2 - n3
if n4 < 0:
continue
calc_PA = (n1 + 2 * n2 + n4) / total_points
calc_PB = (n1 + 2 * n2 + n4) / total_points
calc_PC = (n1 + 2 * n2 + n4) / total_points
calc_PAB = (n2 + n4) / total_points
calc_PAC = (n2 + n4) / total_points
calc_PBC = (n2 + n4) / total_points
# 条件を満たすか確認
if (abs(calc_PA - PA) < 1e-9 and
abs(calc_PB - PB) < 1e-9 and
abs(calc_PC - PC) < 1e-9 and
abs(calc_PAB - PAB) < 1e-9 and
abs(calc_PAC - PAC) < 1e-9 and
abs(calc_PBC - PBC) < 1e-9):
current_PABC = n4 / total_points
valid_probabilities.append(current_PABC)
if current_PABC < min_value:
min_value = current_PABC
min_combination = (n1, n2, n3, n4)
if current_PABC > max_value:
max_value = current_PABC
max_combination = (n1, n2, n3, n4)
# 最小値と最大値を表示
min_PABC = min_value if valid_probabilities else None
max_PABC = max_value if valid_probabilities else None
# 結果の表示
print(f"最小値: {min_PABC}")
print(f"最大値: {max_PABC}")
print(f"最小値を取るときのN1, N2, N3, N4: {min_combination}")
print(f"最大値を取るときのN1, N2, N3, N4: {max_combination}")
最小値: 0.375
最大値: 0.4375
最小値を取るときのN1, N2, N3, N4: (0, 3, 1, 6)
最大値を取るときのN1, N2, N3, N4: (1, 2, 0, 7)