ホーム » 確率母関数
「確率母関数」カテゴリーアーカイブ
和みLab
アーカイブ
カテゴリー
確率母関数の不等式
不等式![]() を可視化して確認します。ここでは二項分布で試してみましょう。
を可視化して確認します。ここでは二項分布で試してみましょう。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # 二項分布の試行回数
p = 0.5 # 二項分布の成功確率
t_values = [0.001, 0.2, 0.4, 0.6, 0.8, 1] # t の値のリスト
sample_size = 10000 # サンプル数
r_values = np.arange(0, n+1, 1) # r の範囲を設定
# 確率母関数 G_X(t) の定義
def G_X(t, n, p):
return (p * t + (1 - p))**n
# 1. 二項分布から乱数を生成
samples = np.random.binomial(n, p, sample_size)
# 2. r に対する P(X <= r) の推定(左辺)
P_X_leq_r_values = [np.sum(samples <= r) / sample_size for r in r_values]
# サブプロットの作成
fig, axes = plt.subplots(2, 3, figsize=(15, 8)) # 2行3列のサブプロットを作成
# 3. 各 t に対するグラフを描画
for i, t in enumerate(t_values):
row = i // 3 # 行番号
col = i % 3 # 列番号
# 右辺 t^{-r} G_X(t) の計算
G_X_value = G_X(t, n, p) # 確率母関数の t 固定
right_hand_side_values = [G_X_value if t == 1 else t**(-r) * G_X_value for r in r_values] # t = 1 の場合はべき乗を回避
# グラフの描画
ax = axes[row, col]
ax.plot(r_values, P_X_leq_r_values, label="P(X <= r) (左辺)", color="blue", linestyle="--")
ax.plot(r_values, right_hand_side_values, label="t^(-r) G_X(t) (右辺)", color="red")
ax.set_title(f"t = {t}")
ax.set_xlabel("r")
ax.set_ylabel("値 (対数スケール)")
ax.set_yscale('log') # 縦軸を対数スケールに設定
ax.legend()
ax.grid(True, which="both", ls="--")
# サブプロット間のレイアウト調整
plt.tight_layout()
plt.show()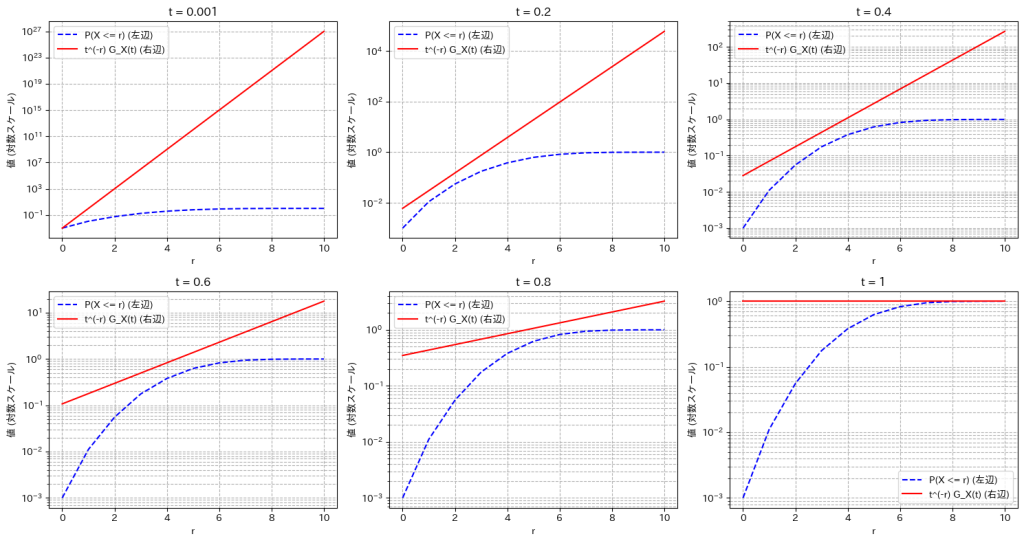
不等式![]() が成り立っていることが確認できます。
が成り立っていることが確認できます。
次に、Xが二項分布B(n,p)に従うとき、aを実数、0<a<pに対し、不等式![]() が成り立つのか可視化しましょう。
が成り立つのか可視化しましょう。
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
# パラメータ設定
n_values = [10, 30, 50] # 試行回数 n のリスト
p_values = [0.3, 0.5, 0.7] # 成功確率 p のリスト
a_values = np.linspace(0.01, 0.99, 50) # a の範囲
# サブプロットの作成
fig, axes = plt.subplots(3, 3, figsize=(15, 15)) # 3x3のグリッドでグラフを描画
# グラフの描画ループ
for i, n in enumerate(n_values):
for j, p in enumerate(p_values):
# 左辺と右辺の値を格納するリスト
left_side_values = []
right_side_values = []
for a in a_values:
# 左辺:P(X <= an) の計算
k = int(np.floor(a * n))
left_side = binom.cdf(k, n, p)
left_side_values.append(left_side)
# 右辺の計算
right_side = (p / a) ** (a * n) * ((1 - p) / (1 - a)) ** ((1 - a) * n)
right_side_values.append(right_side)
# グラフの描画(対数スケール)
ax = axes[i, j]
ax.plot(a_values, left_side_values, label='左辺 $P(X \leq an)$', color='blue')
ax.plot(a_values, right_side_values, label='右辺', color='red', linestyle='--')
# 0 < a < p の範囲に色を塗る
ax.axvspan(0, p, color='yellow', alpha=0.3, label="0<a<pの範囲")
ax.set_title(f'n={n}, p={p}')
ax.set_xlabel('$a$')
ax.set_ylabel('値 (対数スケール)')
ax.set_yscale('log') # 縦軸を対数スケールに設定
ax.legend()
ax.grid(True, which="both", ls="--") # 対数スケールのグリッド
# サブプロット間のレイアウト調整
plt.tight_layout()
plt.show()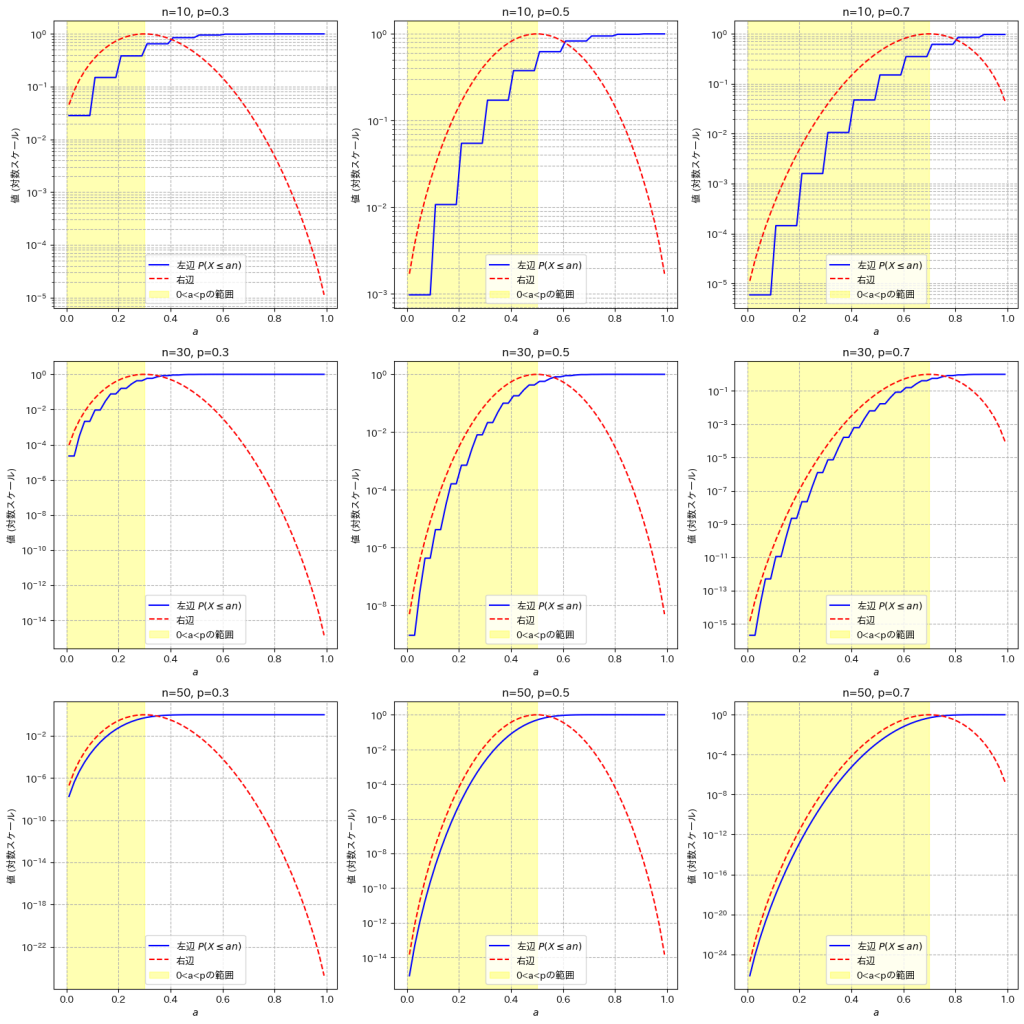
不等式![]() は0<a<pの範囲で成り立っていることが確認できました。
は0<a<pの範囲で成り立っていることが確認できました。
確率母関数の微分と二階微分
二項分布の確率母関数![]() 、その1階微分
、その1階微分 ![]() 、および2階微分
、および2階微分 ![]() を視覚的に比較してみます。
を視覚的に比較してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative
# パラメータ設定
n = 10 # 試行回数
p = 0.5 # 成功確率
# 確率母関数 G_X(t)
def G_X(t, n, p):
return (p * t + (1 - p))**n
# 1階微分 G'_X(t)
def G_X_diff_1(t, n, p):
return derivative(lambda t: G_X(t, n, p), t, dx=1e-6)
# 2階微分 G''_X(t)
def G_X_diff_2(t, n, p):
return derivative(lambda t: G_X_diff_1(t, n, p), t, dx=1e-6)
# t の範囲を定義
t_values = np.linspace(0, 1, 100)
# G_X(t), G'_X(t), G''_X(t) の値を計算
G_X_values = [G_X(t, n, p) for t in t_values]
G_X_diff_1_values = [G_X_diff_1(t, n, p) for t in t_values]
G_X_diff_2_values = [G_X_diff_2(t, n, p) for t in t_values]
# グラフの描画
plt.plot(t_values, G_X_values, label="G_X(t) (確率母関数)", color="blue")
plt.plot(t_values, G_X_diff_1_values, label="G'_X(t) (1階微分)", color="green")
plt.plot(t_values, G_X_diff_2_values, label="G''_X(t) (2階微分)", color="red")
plt.title(f"G_X(t), G'_X(t), G''_X(t) の比較 (n={n}, p={p})")
plt.xlabel("t")
plt.ylabel("値")
plt.legend()
plt.grid(True)
plt.show()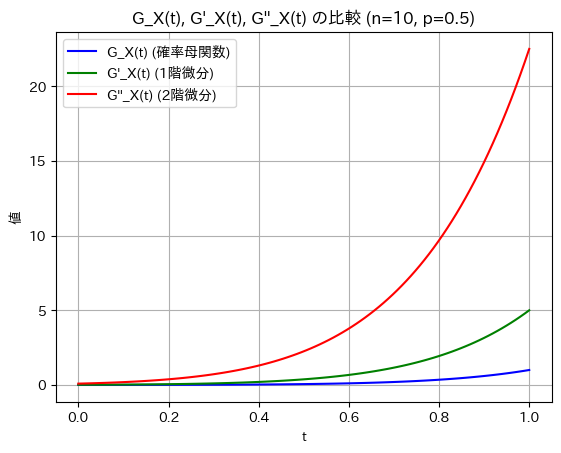
微分を重ねるごとにt=1付近での傾きが急になり大きな値を取っています。期待値や分散などの高次統計量に関連しているため、その値が大きくなっています。